 ベクトル
ベクトル 【予選決勝(1文字固定)法】2変数関数の最大・最小|平方の和(ベクトル利用)の別解
入試頻出。重要問題である、2変数関数の最大値・最小値の求め方。また、ベクトルを利用した別解を紹介。
 ベクトル
ベクトル  2次関数
2次関数  東京大学
東京大学  式と証明
式と証明  2次関数
2次関数  2次関数
2次関数  2次関数
2次関数 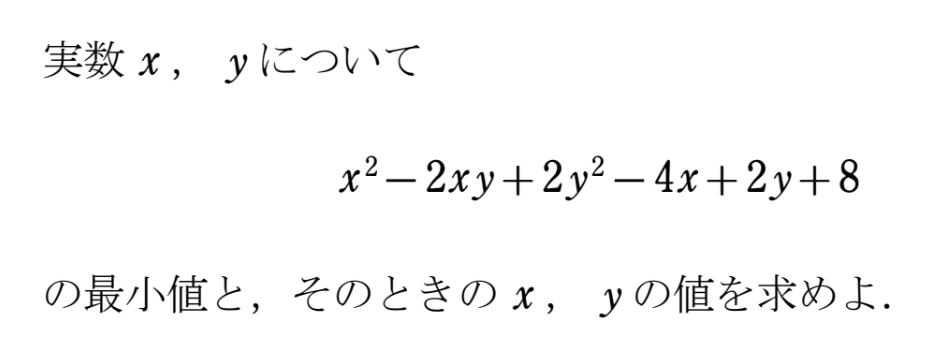 2次関数
2次関数