 共通テスト(センター試験)
共通テスト(センター試験) 2022、2021年度大学入学共通テスト・センター試験過去問|問題・解答・解説
2022、2021年度大学入学共通テスト(数学ⅠAⅡB)過去問の解答・解説まとめ。共通テスト第1日程、第2日程。その他センター試験の一部の過去問の解答・解説。共通テスト対策、演習に!
 共通テスト(センター試験)
共通テスト(センター試験)  分野まとめ
分野まとめ  分野まとめ
分野まとめ  分野まとめ
分野まとめ  分野まとめ
分野まとめ  複素数平面まとめ(数Ⅲ)
複素数平面まとめ(数Ⅲ)  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題 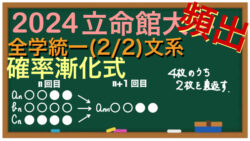 2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  整数問題
整数問題  2023年入試問題
2023年入試問題  2023年入試問題
2023年入試問題  2023年入試問題
2023年入試問題  2023年入試問題
2023年入試問題  整数問題
整数問題  場合の数・確率
場合の数・確率  場合の数・確率
場合の数・確率  共通テスト(センター試験)
共通テスト(センター試験)  2023年入試問題
2023年入試問題  2023年入試問題
2023年入試問題  2023年入試問題
2023年入試問題  複素数と方程式
複素数と方程式  数列
数列  2023年入試問題
2023年入試問題  2023年入試問題
2023年入試問題  2022年入試問題
2022年入試問題  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報