2変数関数の最大値・最小値
【問題】
\(0≦x≦1\)、\(0≦y≦1\)の範囲で、
\((x-2y+1)^2+(x+y-1)^2\) の最大値と最小値を求めよ.
2変数関数の考え方について
2変数関数のMax・min
👉1文字固定(予選決勝法)
2変数関数の最大・最小値に関する基本的な考え方に、予選決勝法と言うものがあります。
これは受験数学では有名解法であり、様々な分野で出題されます。
今まで一度も2変数関数について扱ったことがない人は、
を一度ご覧ください。基本的な考え方を例題を交えて説明しています。
\((x-2y+1)^2+(x+y-1)^2\) の最小値
\((x-2y+1)^2+(x+y-1)^2≧0\) より
\(\begin{cases}x-2y+1=0\\x+y-1=0\end{cases}\)
よって、\(( x , y )=\left(\displaystyle\frac{1}{3} , \displaystyle\frac{2}{3} \right)\) のとき最小値:\(0\)
\((x-2y+1)^2+(x+y-1)^2\) の最大値
\(f( x , y )=(x-2y+1)^2+(x+y-1)^2\) とおく.
\(f( x , y )=2x^2-2xy+5y^2-6y+2\)
\(y\) を固定して考える( \(x\) の \(2\) 次関数だと思って計算する)
\(f( x , y )=2\left(x-\displaystyle\frac{y}{2}\right)^2+\displaystyle\frac{9}{2}y^2-6y+2\)
\(0≦y≦1\) より、軸 \(x=\displaystyle\frac{y}{2}\) は \(0≦\displaystyle\frac{y}{2}≦\displaystyle\frac{1}{2}\) であり、\(0≦x≦1\) より
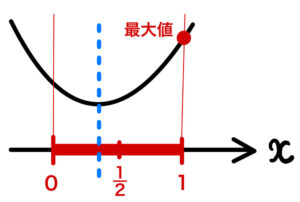
\(x=1\) のとき最大値:\(f( 1 , y )=5y^2-8y+4\)
\(y\) を固定を解除!
\(f( 1 , y )=5y^2-8y+4\) より
\(f( 1 , y )=5\left(y-\displaystyle\frac{4}{5}\right)^2+\displaystyle\frac{4}{5}\)
\(0≦y≦1\) より、
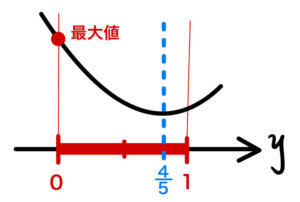
\(y=0\) のとき最小値:\(f( 1 , 0 )=4\)
したがって、\(( x , y )=( 1 , 0 )\) のとき最大値:\(4\)
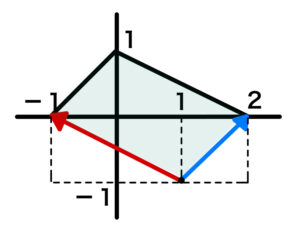
【別解】平方の和の利用
【問題】
\(0≦x≦1\)、\(0≦y≦1\)の範囲で、
\((x-2y+1)^2+(x+y-1)^2\) の最大値と最小値を求めよ.








コメント