 場合の数・確率
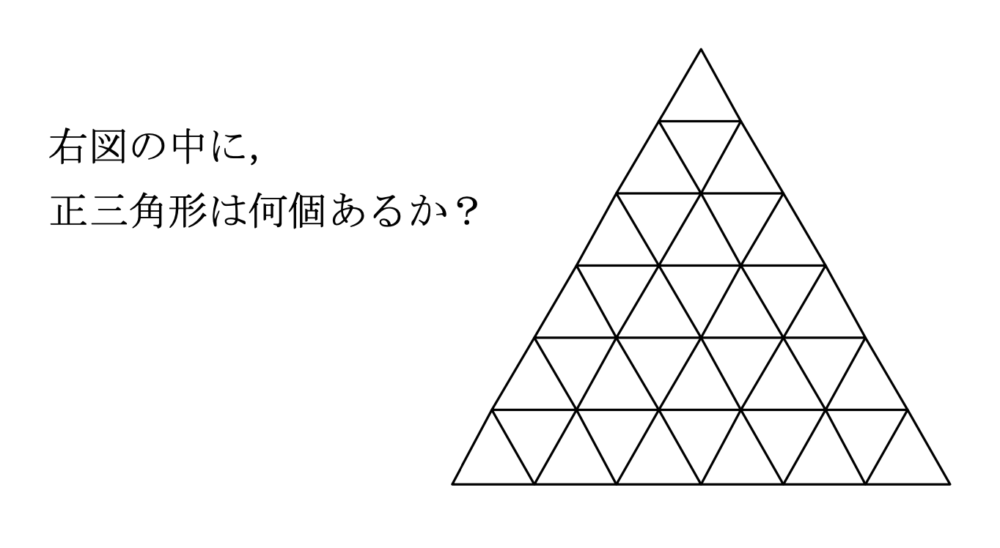
場合の数・確率 【場合の数】何となくでは絶対にダメ!考え方、規則、数え方を正しく学ぶ1問
正三角形が何個あるか?という小学生でも解ける場合の数の問題を、しっかりと数え上げるための良問。場合の数において最も重要なのは数え上げ。ただ闇雲に数えていては数え漏れ、重複が生じます。しっかりと数え上げるための考え方を学ぶための1問です。
 場合の数・確率
場合の数・確率  図形と方程式
図形と方程式  京都大学
京都大学  整数問題
整数問題  整数問題
整数問題  ベクトル
ベクトル  数学(大学入試問題)
数学(大学入試問題) 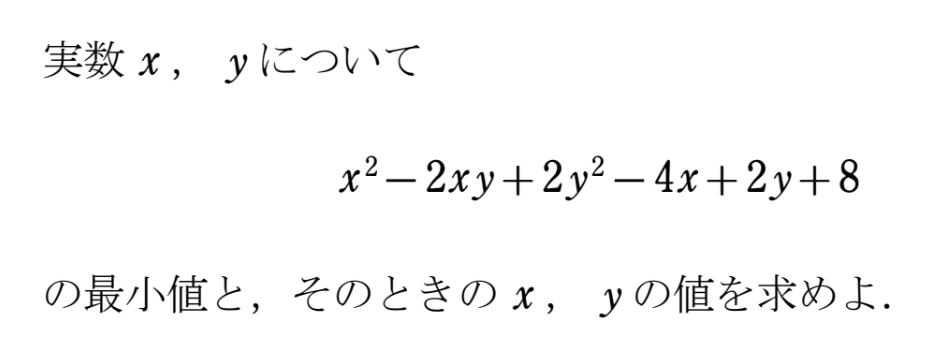 2次関数
2次関数 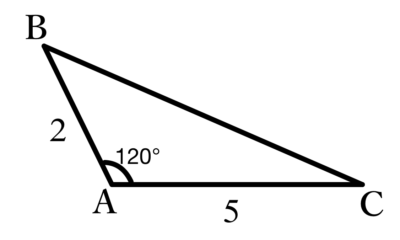 ベクトル
ベクトル  数学(大学入試問題)
数学(大学入試問題)