前回、合同式の性質を確認しました。
基本性質に不安がある人は
合同式とは？合同式の基本性質を理解し、使えるようにする
合同式とは？２次試験（数学）の整数の分野で合同式が使えるかどうかは大きな差がつきます。合同式を知らない、初めて習った人のための基本性質のまとめ。
mathmathmanabu.com
2021.07.15
を確認してください。
整数問題を扱う上で、合同式は必須アイテムです！
さて、ここでは基本的な問題を使って、実際に合同式を利用する練習をしていきます。
合同式を利用した問題を扱う上で、
合同式を使う
👉 とにかく小さい数にする！(理想は \(1\) に！ )
ことを意識しながら解いていきましょう。
問題①
(１) \(37^{100}\) を \(6\) で割った余りを求めなさい．
(２) \(13^{100}\) を \(9\) で割った余りを求めなさい．
解答①
(2) \(9\) を法として
\(13≡4\) より (← \(4\) より小さい数にしたい！)
\(13^2≡4^2=16≡7\) (← \(7\) となり失敗)
\(13^3≡4^3=64≡1\) (← \(1\) となり理想的！) ・・・①
①の両辺を \(33\) 乗すると、
\((13^3)^{33}≡1^{33}=1\)
つまり、\(13^{99}≡1\)
両辺を \(13\) 倍すると、
\(13^{100}≡13≡4\)
したがって、求める余りは \(4\)
問題②
\(n^2\) を \(3\) で割ったときの余りは、\(0\) または \(1\) となることを示せ．
３で割った余り
👉 mod３ で考える
解答②
問題③
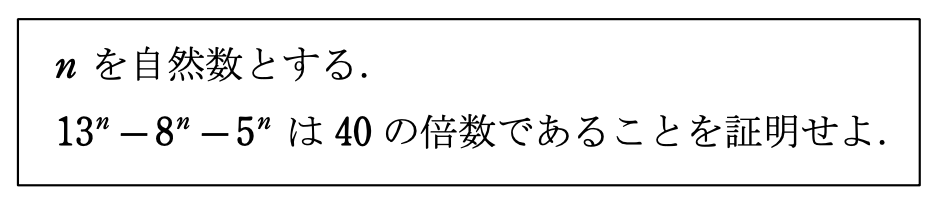
４０の倍数
👉５の倍数 かつ ８の倍数
👉mod５ と mod８ を考える
解答③
問題③は二項定理などの別解もあります。
しかし合同式を利用する方が解答がシンプルになるため、合同式を利用した。
2018 京都大学 整数問題にチャレンジ
2018京都大学｜n^3-7n+9が素数となるn(文系第３問、理系第２問)
素数に関する有名頻出問題。数学の２次試験で差がつきやすい整数分野の問題について、ただ答えが出せるだけの勉強ではなく、どのように考えるのか、思考過程を丁寧に解説。同じ問題は出ませんが、同じ形式の問題は出題されます。しっかりと考え方を学び、２次数学でしっかり得点源に！
mathmathmanabu.com
2021.07.19
コメント