
合同式とは? modとは?
そもそも学校の授業で扱っていない人も多いかもしれません。
しかし2次試験(整数の分野)において、合同式を知っているかどうかは大きな差になります。
ここではまず合同式とは何か?どのような性質があるか、基本を抑えるためのページです。
公式は大丈夫!と言う人は、


にチャレンジ!
合同式とは?(具体例で意味を理解し、使いこなそう!)
合同式とは

と言われても・・・よく分からない・・・。
簡単に言うと
合同式
➡割り算の余りに注目した式
具体的な例で考えましょう!
「10を3で割った余りは1」、「7を3で割った余りは1」 なので、
「10を3で割った余り」=「7を3で割った余り」が成立。
➡ 「10 ≡ 7 (mod 3)」というルール
同様に、\(10≡7≡4≡1\) ( \(mod 3\) ) と言うことになります!
これを文字で一般的に

合同式は必要?
そもそも何のために合同式を利用するのか?
- 解答の表記が簡略化される
- 複雑な問題において、思考の助けとなる
「(10を3で割った余り)と(7を3で割った余り)が等しい」と言うことを「10≡7 ( mod 3 )」とシンプルに表記できます。たったこれだけ?と言われそうですが、複雑な問題になればなるほど効果は絶大!
また、表記が簡略化されるため、余計な情報が削られ、思考を伴う問題においてもメリットが見られます。
整数問題を扱う上で、合同式は必須アイテムです!
合同式の性質について
おえておきたい4つの性質
足し算
・10≡7 ( mod 3 ) ・・・ ① [(10を3で割った余り)=(7を3で割った余り)]
・4≡1 ( mod 3 ) ・・・ ② [(4を3で割った余り)=(1を3で割った余り)]
ここで①+②を考えてみます。
左辺について「10+4を3で割った余りは2」
右辺について「7+1を3で割った余りは2」
となり等しいので
10+4≡7+1 ( mod 3 ) となる.
これを文字で表すと
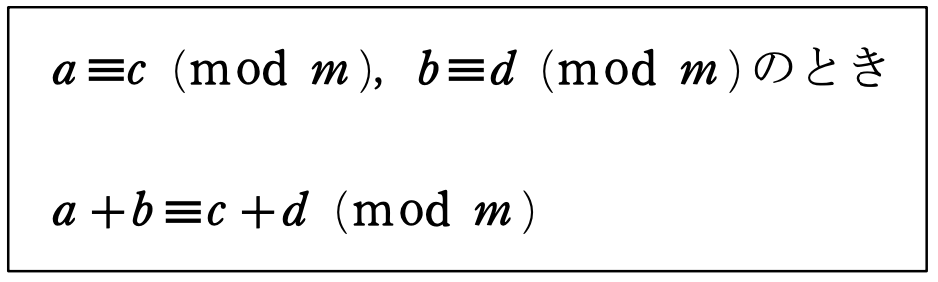
引き算
・10≡7 ( mod 3 ) ・・・ ① [(10を3で割った余り)=(7を3で割った余り)]
・4≡1 ( mod 3 ) ・・・ ② [(4を3で割った余り)=(1を3で割った余り)]
ここで①ー②を考えてみます。
左辺について「10-4を3で割った余りは0」
右辺について「7-1を3で割った余りは0」
となり等しいので
10-4≡7-1 ( mod 3 ) となる.
これを文字で表すと
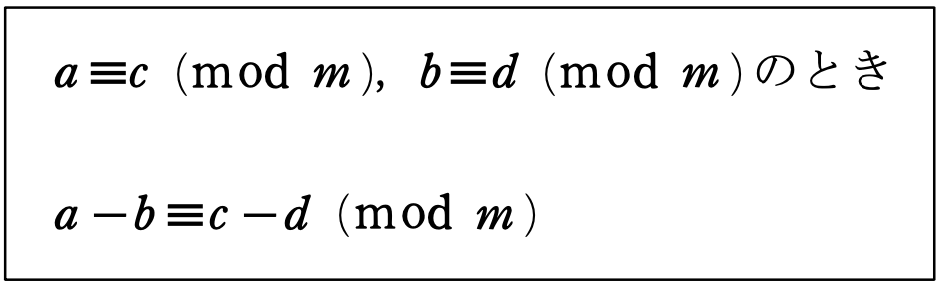
かけ算
・10≡7 ( mod 3 ) ・・・ ① [(10を3で割った余り)=(7を3で割った余り)]
・4≡1 ( mod 3 ) ・・・ ② [(4を3で割った余り)=(1を3で割った余り)]
ここで①×②を考えてみます。
左辺について「10×4を3で割った余りは1」
右辺について「7×1を3で割った余りは1」
となり等しいので
10×4≡7×1 ( mod 3 ) となる.
これを文字で表すと
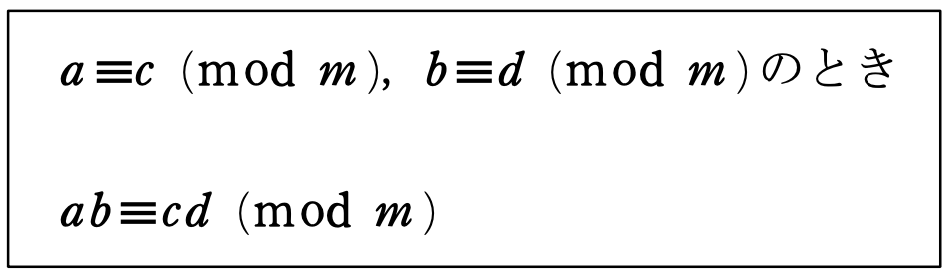
累乗(これはよく使う!)
上の掛け算の性質において、①×②➡①×①と考える(②を①に置き換える)
すると
10×10≡7×7 ( mod 3 ) となる.
つまり
102 ≡72 ( mod 3 ) ・・・③
次に①×③を考えると
103 ≡73 ( mod 3 )
あとはこれを繰り返すことで
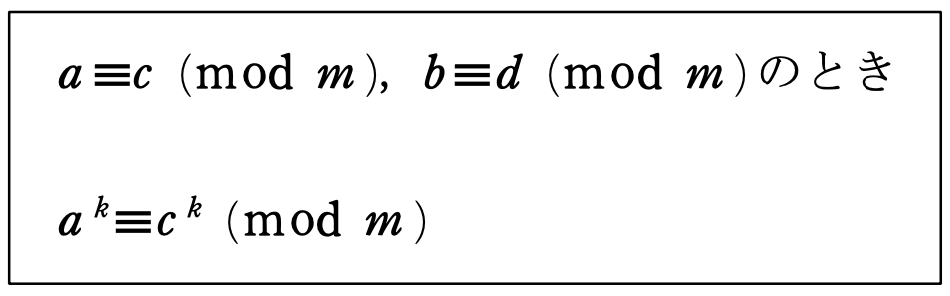
4つの性質まとめ

わり算について(要注意)
合同式の計算は、割り算以外は基本的に普通に計算して良いと言うことだったが、割り算に関しては使用できるときに制限がある。

具体例
「2×10を3で割った余りは2」
「2×7を3で割った余りは2」
となり等しいので、
2×10≡2×7 ( mod 3 ) となる。
この両辺を2で割ると
10≡7 ( mod 3 ) となり、この式は成立。
※2と3は互いに素であるから成立した!
「6×10を3で割った余りは0」
「6×9を3で割った余りは0」
となり等しいので、
6×10≡6×9 ( mod 3 ) となる。
この両辺を6で割ると
10≡9 ( mod 3 ) となるがこの式は成立しない。
※6と3は互いに素でないため成立しない!
最初のうちは使わないことをお勧めします。
合同式に慣れ、使いこなせるようになってから使用するように!
基本的な性質をしっかり確認できたら、


にチャレンジしましょう!







コメント