【2023京都大学・理系・第5問】
\(O\) を原点とする \(xyz\) 平面において,点 \(P\) と点 \(Q\) は次の \(3\) つの条件 (\(a\)),(\(b\)),(\(c\)) を満たしている.
(\(a\)) 点 \(P\) は \(x\) 軸上にある.
(\(b\)) 点 \(Q\) は \(yz\) 平面上にある.
(\(c\)) 線分 \(OP\) と線分 \(OQ\) の長さの和は \(1\) である.
点 \(P\) と点 \(Q\) が条件 (\(a\)),(\(b\)),(\(c\)) を満たしながらくまなく動くとき,線分 \(PQ\) が通過してできる立体の体積を求めよ.
解答・解説
求める立体は,\(-1≦x≦1\) の範囲にあり,\(yz\) 平面に関して対称な立体なので
\(0≦x≦1\) の体積を求めて,\(2\) 倍すればよい.
\(P(p,0,0)\) とおく.( \(0≦p≦1\) )
条件 (\(c\)) より \(OQ=1-p\)
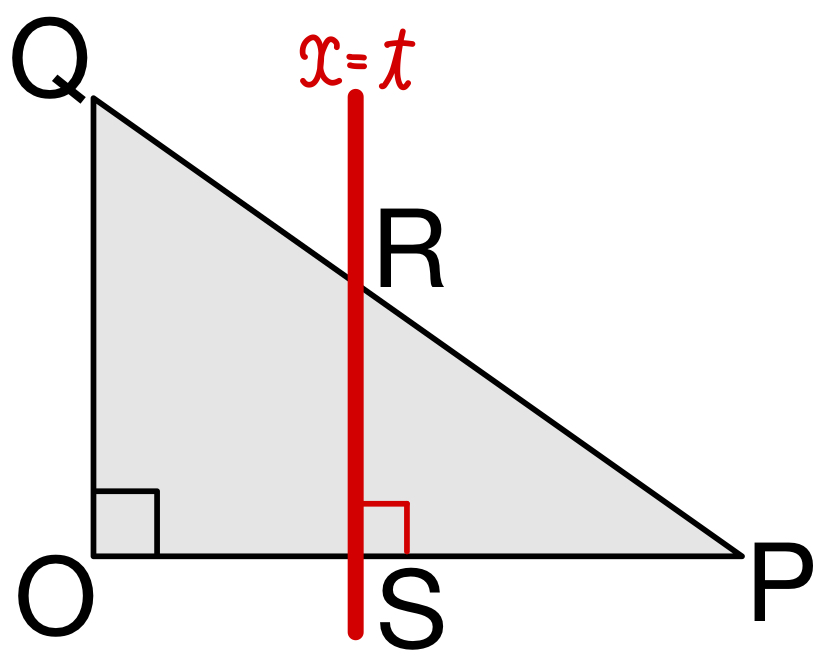 ここで平面 \(x=t\) ( \(0≦t≦p\) ) と線分 \(PQ\) の共有点を \(R\) とし,
ここで平面 \(x=t\) ( \(0≦t≦p\) ) と線分 \(PQ\) の共有点を \(R\) とし,
点 \(R\) から \(x\) 軸に下ろした垂線の足を \(S\) とすると
\(\triangle PRS\) と \(\triangle PQO\) は相似な図形であるから
\(PS\):\(SR=PO\):\(OQ\)
\(p-t\):\(SR=p\):\(1-p\)
\(SR=\displaystyle\frac{(p-t)(1-p)}{p}=-p-\displaystyle\frac{t}{p}+t+1\)
\(f(p)=-p-\displaystyle\frac{t}{p}+t+1\) ( \(t≦p≦1\) ) とおく.
\(f^{\prime}(p)=-1+\displaystyle\frac{t}{p^2}=\displaystyle\frac{t-p^2}{p^2}\)
| \(p\) | \(t\) | \(\sqrt{t}\) | \(1\) | ||
| \(f^{\prime}(p)\) | + | \(0\) | ー | ||
| \(f(p)\) | \(0\) | ↗️ | (極大) | ↘️ | \(0\) |
よって,\(p=\sqrt{t}\) で \(f(p)\) は
最大値:\(\left(1-\sqrt{t}\right)^2\) をとる.
ゆえに,線分 \(PQ\) が通過してできる立体を \(T\) とすると
\(T\) の平面 \(x=t\) による断面は
半径 \(\left(1-\sqrt{t}\right)^2\) の円の周および内部
したがって求める体積 \(V\) は
\(V=2\displaystyle\int^{1}_{0}\pi \left\{\left(1-\sqrt{t}\right)^2\right\}^2dt\)
\(=2\pi\displaystyle\int^{1}_{0} \left(t^2-4t^{\frac{3}{2}}+6t-4t^{\frac{1}{2}}+1\right)dt\)
\(=2\pi\Bigl[\displaystyle\frac{1}{3}t^3-\displaystyle\frac{8}{5}t^{\frac{5}{2}}+3t^2-\displaystyle\frac{8}{3}t^{\frac{3}{2}}+t\Bigr]^{1}_{0}\)
\(=\displaystyle\frac{2}{15}\pi\)







コメント