【2023数学ⅠA(第1日程)】第５問(図形の性質)

(１)問題と解答・解説《ア〜カ》

(１)解答・解説《ア〜カ》

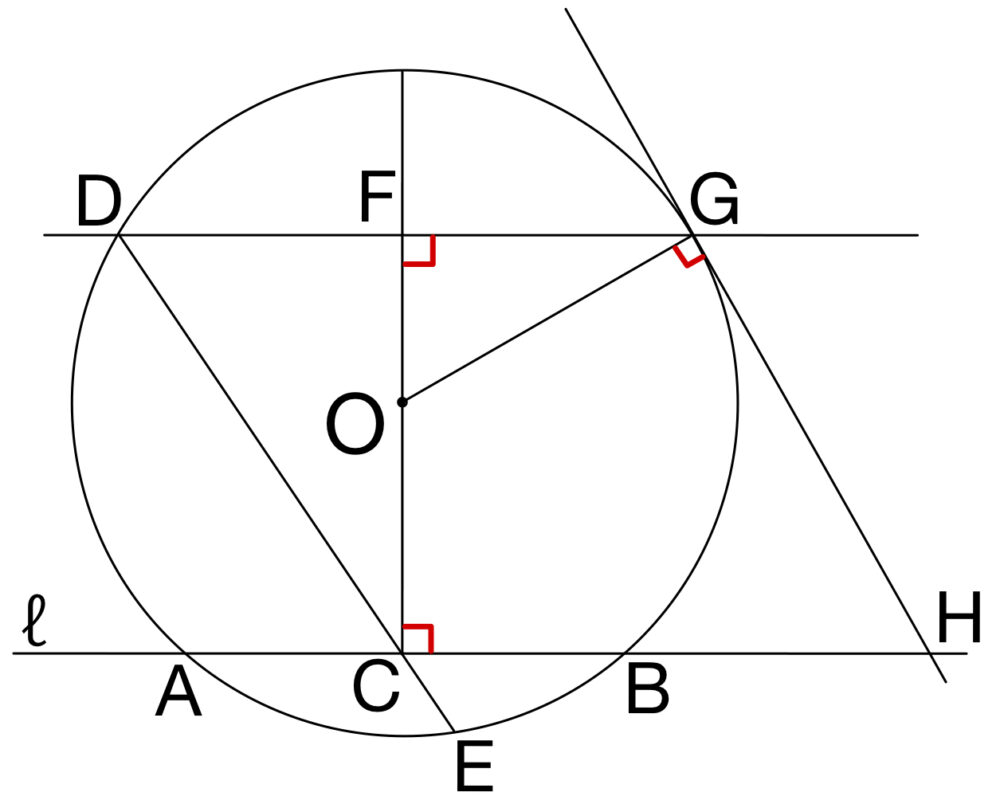点 \(C\) は \(AB\) の中点より，\(OC\perp AB\)

よって，\(\angle OCH=90°\) ・・・①

また，直線 \(GH\) は点 \(G\) における円 \(O\) の接線なので

\(\angle OGH=90°\) ・・・②

したがって，①，②から対角の和が \(180°\) より

\(4\) 点 \(C\)，\(G\)，\(H\)，\(O\) は同一円周上・・・《ウ：③》

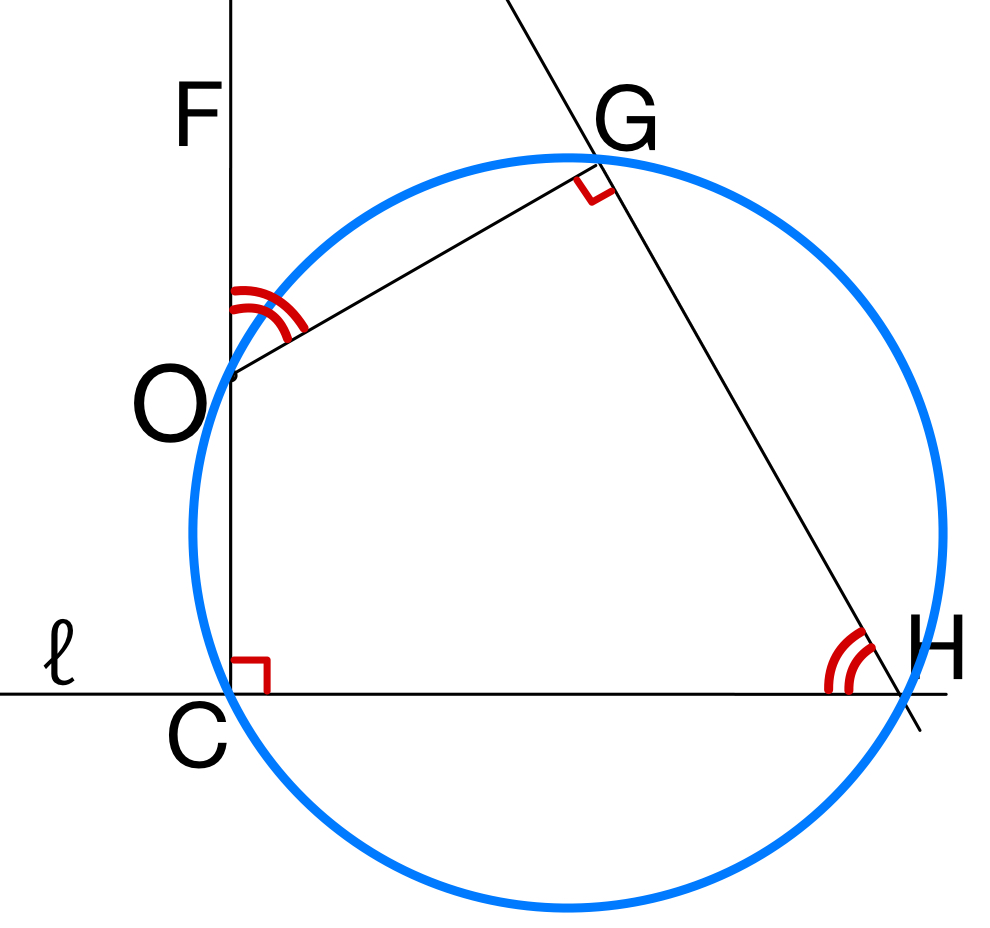円に内接する四角形の \(1\) つの内角と，その対角の外角は等しいので，

\(\angle CHG=\angle FOG\) ・・・《エ：④》

一方，点 \(E\) は円 \(O\) の周上にあることから

中心角と円周角の関係より

\(\angle DOG=2\angle DEG\) ・・・③

また，(Step3)より \(DG\) \(//\) \(\ell\) で，\(OF \perp DG\) となるので

点 \(F\) は \(DG\) の中点となる．

よって，\(\angle FOG=\angle FOD\) ・・・④

③，④より

\(\angle DOG=2\angle FOG=2\angle DEG\)

よって，\(\angle FOG=\angle DEG\) ・・・《オ：③》

\(\angle CHG=\angle DEG\) であるので，

円周角の定理の逆より

\(4\) 点 \(C\)，\(G\)，\(H\)，\(E\) は同一円周上・・・《カ：②》

したがって，この円が点 \(O\) を通ることより，

\(\angle OEH=\angle OCH=90°\) を示すことができる．

(２)問題と解答・解説《キ〜サ》

(２)解答・解説《キ〜サ》

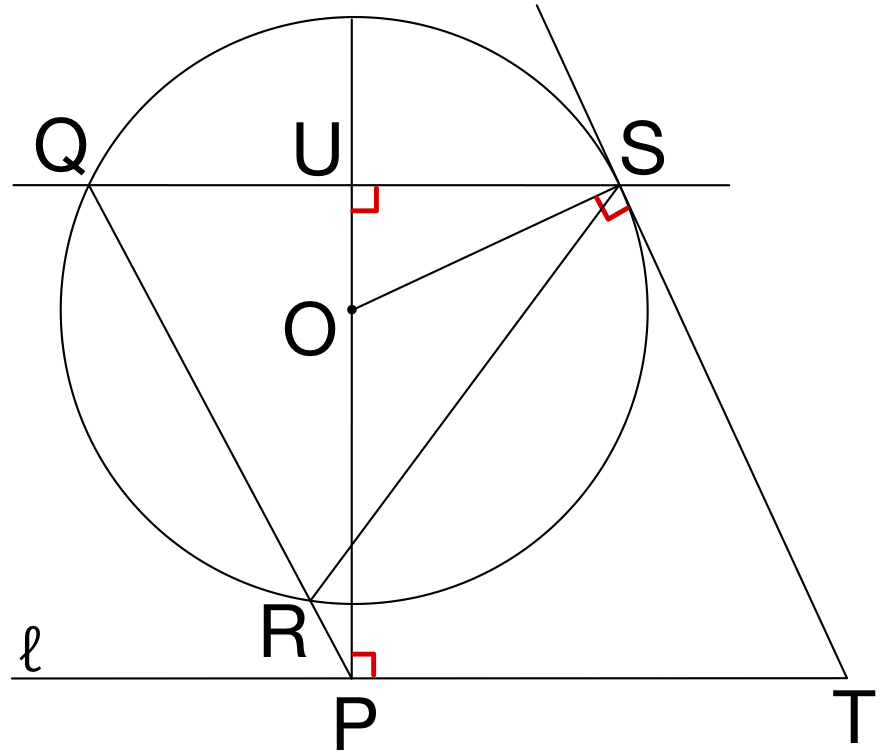直線 \(OP\) と直線 \(QS\) ( \(QS\) の中点 ) を \(U\) とおく．

(１)と同様に考えると

\(\angle OPT=\angle OST=90°\) より

\(4\) 点 \(O\)，\(P\)，\(T\)，\(S\) は同一円周上にあるので

\(\angle PTS=\angle UOS\)

また，\(\angle UOS=\angle UOQ\) であり，

円周角と中心角の定理の関係から

\(\angle QOS=2\angle QRS\)

以上から，\(\angle PTS=\angle QRS\) ・・・《キ：③》

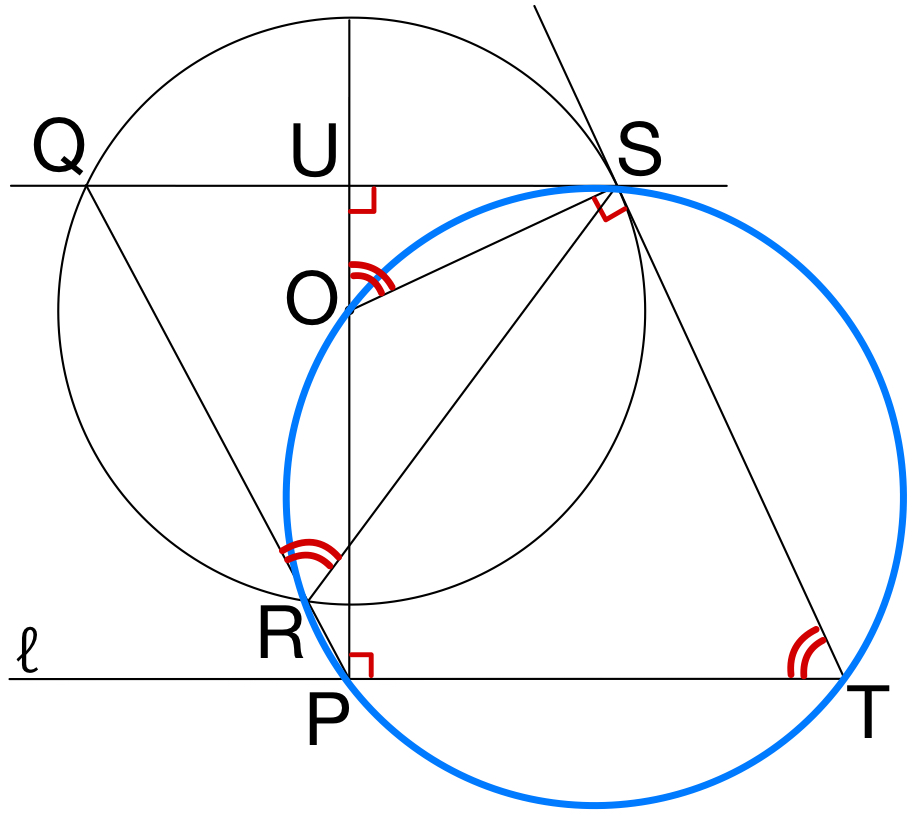よって，\(5\) 点 \(O\)，\(R\)，\(P\)，\(T\)，\(S\) は同一円周上にあり，

\(\angle OPT=\angle OST=90°\) より

直径が \(OT\) の円となる．

したがって，\(OT=3\sqrt{6}\) のとき

この円の半径は \(\displaystyle\frac{3\sqrt{6}}{2}\) ・・・《ク〜コ》

また，円周角の定理から \(\angle OPT=\angle ORT=90°\) より

\(\triangle ORT\) で三平方の定理より

\(OR^2+RT^2=OT^2\)

円 \(O\) の半径が \(\sqrt{5}\) で，\(OT=3\sqrt{6}\) より

\(\sqrt{5}^2+RT^2=(3\sqrt{6})^2\)

\(RT>0\) より，\(RT=7\) ・・・《サ》