
数学Aの場合の数の分野を苦手とする人が非常に多い。
特に数学Aが苦手な人は、とりあえず P やら C やらを使いたがります。
もちろんそれはそれで大切ですが、一番大切なのはしっかりと数え上げる力を養うこと!
しかし闇雲に数え上げをしても大抵の場合は失敗します。漏れなく、数え上げるためには、しっかりと考え方を学び、様々な問題に応用できるようにしていきましょう!
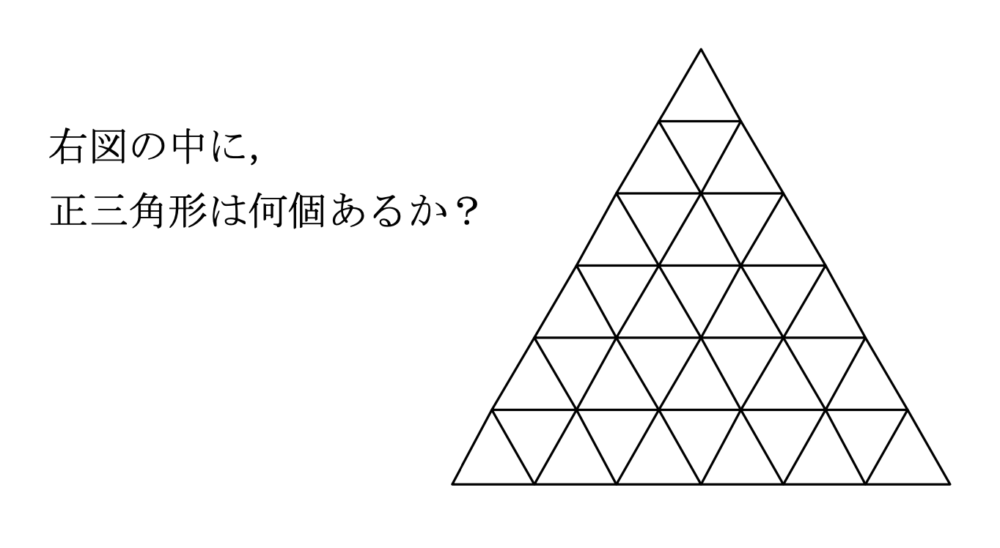
数え上げの考え方
絶対にやってはいけないことは、手当たり次第数え上げること!
大切なのは、
- 自分の中でしっかりとルールを決めて漏れなく数えること。
- 同じ場合を重複していないか確認
- 必要に応じて樹形図などを利用し視覚化する
上のことに気をつけながら問題を解いた上で、結果的に間違えたのであればそれは全然OK!
しかし間違えた場合は、何がダメであったのかをしっかりと分析し、次に繋げましょう。
何となく数えて間違うのは最悪です!!
解説
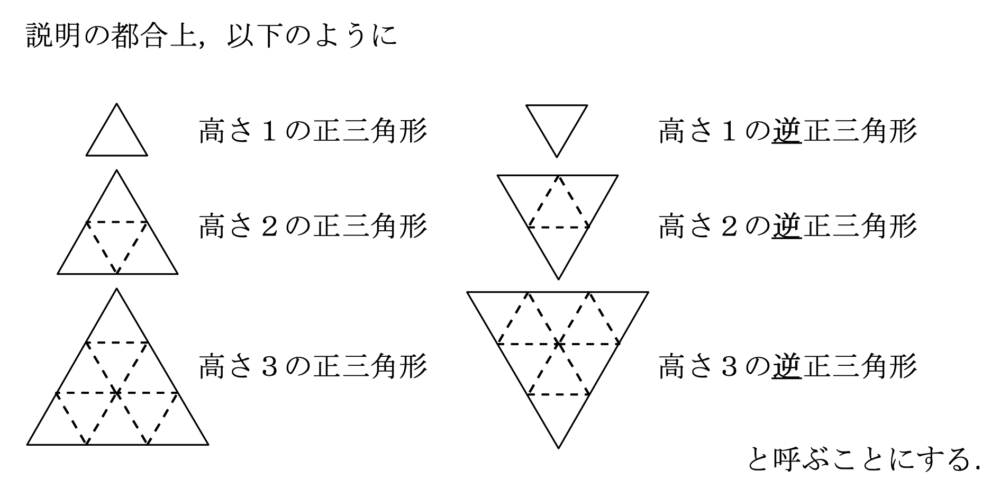
(ア)高さが1の正三角形の個数について
- 上から1段目・・・1個
- 上から2段目・・・2個
- 上から3段目・・・3個
- 上から4段目・・・4個
- 上から5段目・・・5個
- 上から6段目・・・6個 👈 この規則なら何段になってもできる!!
よって 1+2+3+4+5+6=21個
(イ)高さが2の正三角形の個数について
- 上から1〜2段目・・・1個
- 上から2〜3段目・・・2個
- 上から3〜4段目・・・3個
- 上から4〜5段目・・・4個
- 上から5〜6段目・・・5個
よって 1+2+3+4+5=15個
(ウ)高さが3の正三角形の個数について
- 上から1〜3段目・・・1個
- 上から2〜4段目・・・2個
- 上から3〜5段目・・・3個
- 上から4〜6段目・・・4個
よって 1+2+3+4=10個
(エ)高さが4の正三角形の個数について
- 上から1〜4段目・・・1個
- 上から2〜5段目・・・2個
- 上から3〜6段目・・・3個
よって 1+2+3=6個
(オ)高さが5の正三角形の個数について
- 上から1〜5段目・・・1個
- 上から2〜6段目・・・2個
よって 1+2=3個
(カ)高さが6の正三角形の個数について
- 上から1〜6段目・・・1個
よって 1個
(キ)高さが1の逆三角形の個数について
- 上から1段目・・・✖️
- 上から2段目・・・1個
- 上から3段目・・・2個
- 上から4段目・・・3個
- 上から5段目・・・4個
- 上から6段目・・・5個
よって 1+2+3+4+5=15個
(ク)高さが2の逆三角形の個数について
- 上から1〜2段目・・・✖️
- 上から2〜3段目・・・✖️
- 上から3〜4段目・・・1個
- 上から4〜5段目・・・2個
- 上から5〜6段目・・・3個
よって 1+2+3=6個
(ケ)高さが3の逆三角形の個数について
- 上から1〜3段目・・・✖️
- 上から2〜4段目・・・✖️
- 上から3〜5段目・・・✖️
- 上から4〜6段目・・・1個
よって 1個
したがって(ア)〜(ケ)より
21+15+10+6+3+1+15+6+1=78個
まとめ
いかがだったでしょうか?
数学が苦手な人はたくさん場合分けをすることを嫌います。
確かに今回の場合分けはたくさんあります(もっとシンプルにまとめることもできる)が、1つ1つ規則的で、漏れなく、重複なくカウントできる解法です。
中途半端に楽しようとすると逆に数え漏れや重複が生じます。
また今回の解法であれば、問題の三角形がもっと大きな形でも処理できるかと思います。(解法が一般化できる)
多くの問題をこなすことも大切ですが、良問をじっくりと解くことで力がつきますので、ここで得た考え方を入試で生かせるように!
また今後も様々な分野で良問・頻出問題を定期的にアップしていきますので、もしよかったら他の分野の問題も是非チャレンジしてください。
また○○の分野の考え方が知りたいなど、リクエストがありましたらコメント、問い合わせ、またはTwitterでお気軽にご連絡ください。
また、場合の数・確率について「考え方」をまとめた参考書として「ハッとめざめる確率」があります。
何となくで問題を解いている人は特に、この1冊を使って考え方を一度総まとめしてみてください!







コメント