【2007京都大学・甲・第６問】
\(y=xe^{1-x}\) と \(y=x\) のグラフで囲まれた部分を \(x\) 軸周りに回転してできる立体の体積を求めよ．
回転体の体積
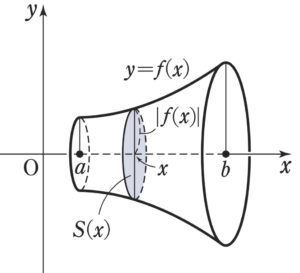\(a<b\) のとき，曲線 \(y=f(x)\) と \(x\) 軸，および \(2\) 直線 \(x=a\) , \(x=b\) で囲まれた部分を，\(x\) 軸の周りに回転させてできる立体の体積 \(V\) は，
\(V=\pi\displaystyle\int^{b}_{a}\left\{f(x)\right\}^2 dx=\pi\displaystyle\int^{b}_{a}y^2 dx\)
解答・解説
\(y=xe^{1-x}\) より
\(y^{\prime}=e^{1-x}+xe^{1-x}\cdot(-1)=(1-x)e^{1-x}\)
よって増減表は，
| \(x\) | … | \(1\) | … |
| \(y^{\prime}\) | ＋ | \(0\) | ー |
| \(y\) | ↗️ | \(1\) | ↘️ |
また，\(y=xe^{1-x}\) と \(y=x\) の交点の \(x\) 座標は
\(xe^{1-x}=x\) \(\iff\) \(x(e^{1-x}-1)=0\)
よって，\(x=0,1\)
したがって，\(y=xe^{1-x}\) と \(y=x\) のグラフの概形は下図のようになり，図の斜線部を \(x\) 軸の周りに回転した体積を求めればよい．
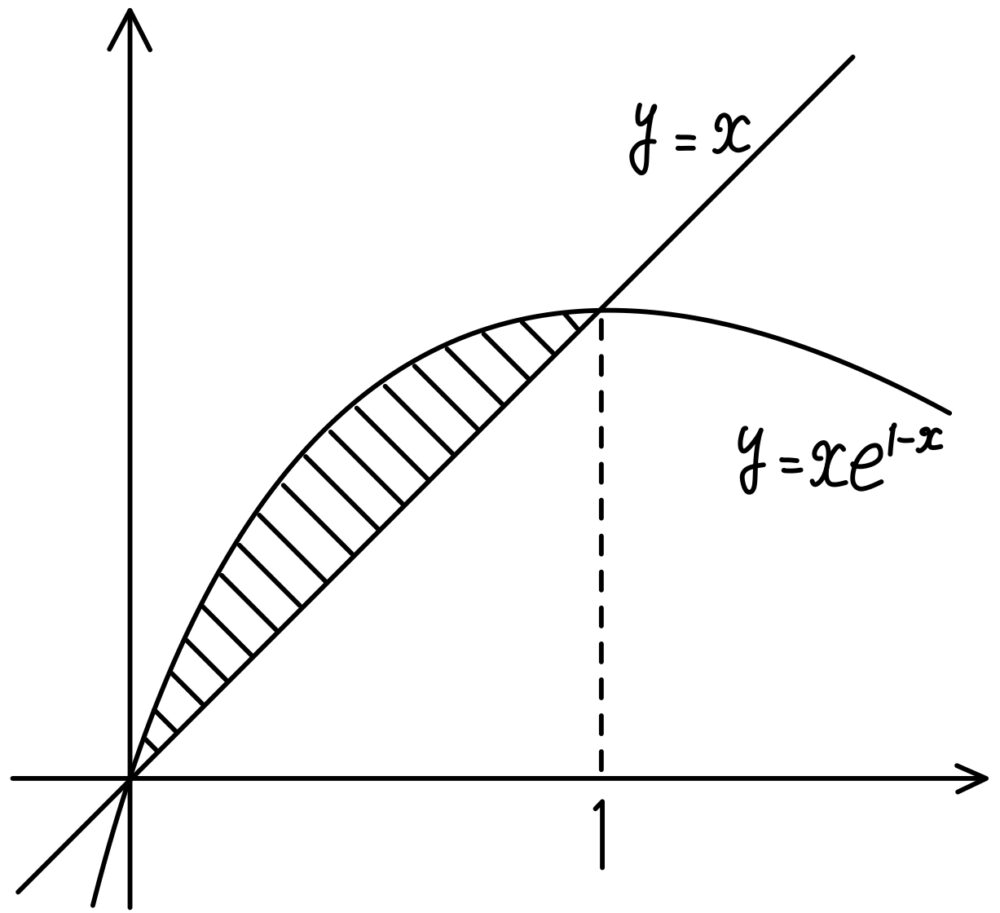
求める体積を \(V\) とすると，
\(V=\pi\displaystyle\int^{1}_{0}\left(xe^{1-x}\right)^2 dx-\pi\displaystyle\int^{1}_{0}x^2 dx\)
\(=\pi e^2\displaystyle\int^{1}_{0}x^2e^{-2x} dx-\pi\displaystyle\int^{1}_{0}x^2 dx\)
ここで，\(I_{1}=\displaystyle\int^{1}_{0}x^2e^{-2x} dx\) , \(I_{2}=\displaystyle\int^{1}_{0}x^2 dx\) とおく．
\(I_{1}=\Bigl[x^2\cdot\left(-\displaystyle\frac{1}{2}e^{-2x}\right)\Bigr]^{1}_{0}-\displaystyle\int^{1}_{0}2x\left(-\displaystyle\frac{1}{2}e^{-2x}\right) dx\)
\(=-\displaystyle\frac{1}{2}e^{-2}+\displaystyle\int^{1}_{0}xe^{-2x} dx\)
\(=-\displaystyle\frac{1}{2}e^{-2}+\Bigl[x\cdot\left(-\displaystyle\frac{1}{2}e^{-2x}\right)\Bigr]^{1}_{0}-\displaystyle\int^{1}_{0}\left(-\displaystyle\frac{1}{2}e^{-2x}\right) dx\)
\(=-\displaystyle\frac{1}{2}e^{-2}-\displaystyle\frac{1}{2}e^{-2}+\displaystyle\frac{1}{2}\Bigl[-\displaystyle\frac{1}{2}e^{-2x}\Bigr]^{1}_{0}\)
\(=\displaystyle\frac{-5e^{-2}+1}{4}\)
\(I_{2}=\Bigl[\displaystyle\frac{1}{3}x^3\Bigr]^{1}_{0}=\displaystyle\frac{1}{3}\)
したがって，
\(V=\pi e^2\displaystyle\frac{-5e^{-2}+1}{4}-\displaystyle\frac{\pi}{3}=\displaystyle\frac{(3e^2-19)\pi}{12}\)
コメント