【2022上智大学・理工】cos61°の近似値｜近似式について

【2022上智大学】

\(\cos 61°\) の近似値を求めよ．

\(y=\cos x\) の \(1\) 次の近似式を用いて計算し，少数第 \(3\) 位を四捨五入せよ．

ただし，\(\pi=3.14\) , \(\sqrt{3}=1.73\) として用いてよい．

近似式について

関数 \(f(x)\) が \(x=a\) で微分可能であるとき，

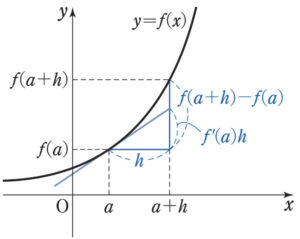\(x=a\) の近くにある \(f(x)\) の値を近似する式について

微分係数 \(f^{\prime}(a)\) は

\(\displaystyle\lim_{h\rightarrow 0} \displaystyle\frac{f(a+h)-f(a)}{h}=f^{\prime}(a)\)

よって，\(| h |\) が十分に小さいとき

\(\displaystyle\frac{f(a+h)-f(a)}{h} ≒ f^{\prime}(a)\)

すなわち，\(f(a+h) ≒ f(a)+f^{\prime}(a)h\)

この式において，\(a=0\) , \(h=x\) とすると，\(| x |\) が十分に小さいとき

\(f(x) ≒ f(0)+f^{\prime}(0)x\)

\(| h |\) が十分に小さいとき \(f(a+h) ≒ f(a)+f^{\prime}(a)h\)

\(| x |\) が十分に小さいとき \(f(x) ≒ f(0)+f^{\prime}(0)x\)

\(f(x)=\cos x\) とおくと，\(f^{\prime}(x)=-\sin x\)

\(| h |\) が十分に小さいとき

\(f\left(\displaystyle\frac{\pi}{3}+h\right) ≒ f\left(\displaystyle\frac{\pi}{3}\right)+f^{\prime}\left(\displaystyle\frac{\pi}{3}\right)h\) より

\(\cos\left(\displaystyle\frac{\pi}{3}+h\right) ≒ \cos\displaystyle\frac{\pi}{3}-\sin\displaystyle\frac{\pi}{3}\cdot h\)

よって，\(\cos\left(\displaystyle\frac{\pi}{3}+h\right) ≒ \displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}h\)

この式に \(h=\displaystyle\frac{\pi}{180}\) を代入すると

\(\cos\left(\displaystyle\frac{\pi}{3}+\displaystyle\frac{\pi}{180}\right) ≒ \displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}\pi}{360}\)

\(\pi=3.14\) , \(\sqrt{3}=1.73\) として計算すると，

\(\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}\pi}{360}=0.484\cdots\)

したがって，小数第 \(3\) 位を四捨五入すると，\(\cos 61° ≒ 0.48\)