【2021千葉大学】
平面上に半径がそれぞれ \(a^2\) , \(b^2\) , \(c^2\) ( \(0<a<b<c\) ) の \(3\) つの円 \(A\) , \(B\) , \(C\) および直線 \(l\) がある.\(3\) つの円はどれも直線 \(l\) に接していて,どの \(2\) つの円も外接しているとする.
(1) \(c\) を \(a\) と \(b\) を用いて表せ.
(2) 数列 \(a\) , \(b\) , \(c\) が等比数列となるとき,その公比を求めよ.
(1)2つの円の位置関係
2つの円の半径を \(r\) , \(r^{\prime}\) ( \(r>r^{\prime}\) ) ,\(2\) 円の中心間の距離を \(d\) とする.
(1) 互いに外部にある
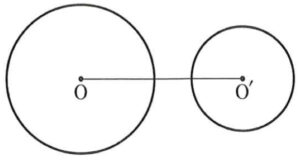
\(r+r^{\prime}>d\)
(2) 外接する(1点を共有する)
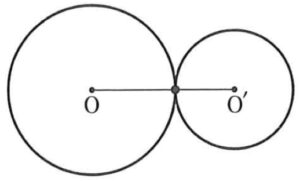
\(r+r^{\prime}=d\)
(3) 2点で交わる
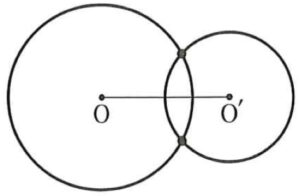
\(r-r^{\prime}<d<r+r^{\prime}\)
(4) 内接する(1点を共有する)
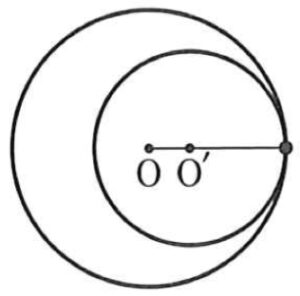
\(r-r^{\prime}=d\)
(5) 一方が他方の内部にある
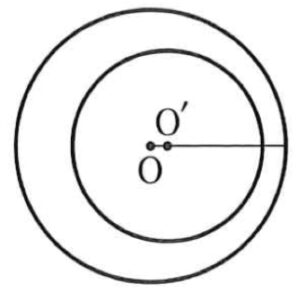
\(r-r^{\prime}>d\)
(1)解答・解説
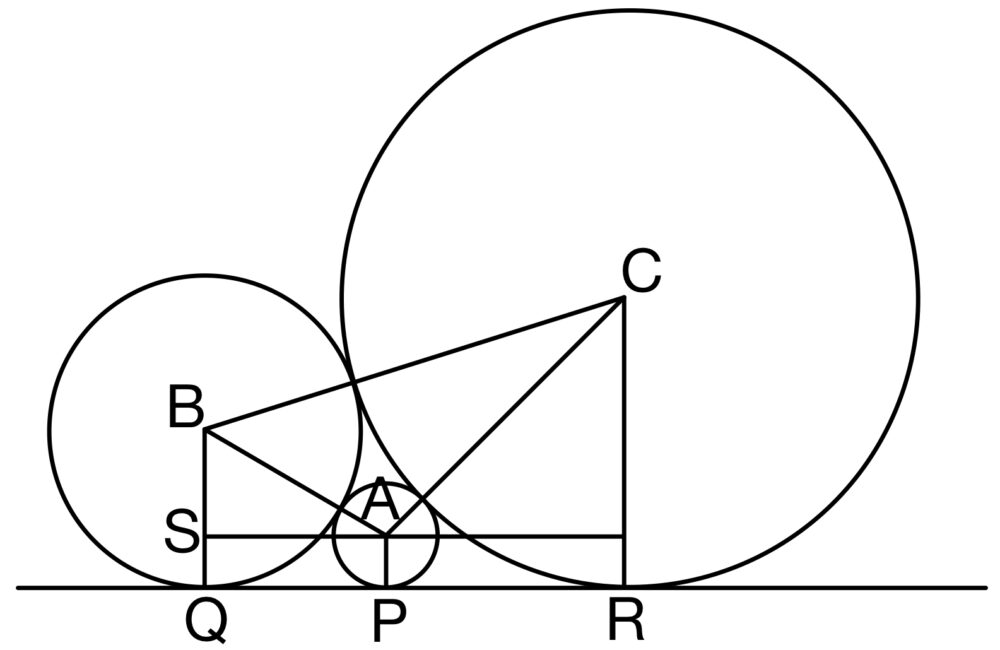
円 \(A\) , \(B\) , \(C\) の中心の座標をそれぞれ \(A\) , \(B\) , \(C\) とし,またその各点から直線 \(l\) に下ろした垂線 \(AP\) , \(BQ\) , \(CR\) とする.
点 \(A\) から線分 \(BQ\) に下ろした垂線を \(AS\) とする.
\(2\) 円 \(A\) , \(B\) は外接するので,\(AB=a^2+b^2\)
また \(BS=BQ-SQ=BQ-AP=b^2-a^2\) であり,
直角三角形 \(ABS\) で三平方の定理から
\(AS=PQ=\sqrt{(a^2+b^2)^2-(b^2-a^2)^2}=2ab\)
同様に考え,\(QR=2bc\) , \(RP=2ca\) となる.
\(PQ+RP=QR\) より
\(2ab+2ca=2bc\)
\((b-a)c=ab\)
よって,\(c=\displaystyle\frac{ab}{b-a}\)
(2)等比中項
※ 数列 \(a\) , \(b\) , \(c\) が等差数列 \(\iff\) \(2b=a+c\)
(2)解答・解説
数列 \(a\) , \(b\) , \(c\) は等比数列より
\(b^2=ac\) ・・・①
①と(1)より
\(b^2=a\cdot\displaystyle\frac{ab}{b-a}\)
式を整理すると
\(b^3-ab^2-a^2b=0\)
\(b(b^2-ab-a^2)=0\)
\(b>0\) であるから,
\(b^2-ab-a^2=0\) ・・・②
ここで,求める公比を \(r\) とおくと
\(b=ar\) ( \(r>1\) ) とおける.
②に代入すると
\(a^2(r^2-r-1)=0\)
\(a>0\) より \(r^2-r-1=0\)
\(r>1\) より
\(r=\displaystyle\frac{1+\sqrt{5}}{2}\)







コメント
数学ど素人の質問です。
b2 = a * ab/b-a を整理して、なぜ b2 -ab -a2 = 0 になるのでしょうか?
私がやると b3 -ab2 – a2b = 0 になってしまいます。
教えていただけると幸いです。
マスマス学ぶの記事をご覧いただき、そしてコメントありがとうございます。
b>0ですので、bで割りました。
説明が省略されており、丁寧でなく申し訳ありません。
追加説明を入れさせていただきました。
今後ともよろしくお願いします。