【2021大分大学・医】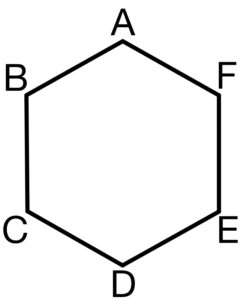
図のような正六角形 \(ABCDEF\) と動点 \(P\) があり,点 \(P\) は最初頂点 \(A\) の位置にある.サイコロを振って,\(1\) ,\(2\) ,\(3\) の目が出れば時計回りに隣の頂点へ移動し,\(4\) ,\(5\) の目が出れば反時計回りに隣の頂点に移動する.そして,\(6\) の目が出たときはその位置にとどまる.
(1) サイコロを \(3\) 回振った時点で点 \(P\) が頂点 \(D\) の位置にある確率を求めよ.
(2) サイコロを \(4\) 回振った時点で点 \(P\) が頂点 \(E\) の位置にある確率を求めよ.
(3) サイコロを \(6\) 回振った時点で点 \(P\) が頂点 \(A\) の位置にある確率を求めよ.
反復試行の確率
さいころを繰り返し \(n\) 回投げる 👉 反復試行
解答・解説
時計回りの移動を \(x\) 回,反時計回りの移動を \(y\) 回,その位置にとどまることを \(z\) 回とする.
(1) サイコロを \(3\) 回振った時点で点 \(P\) が頂点 \(D\) の位置にある確率
\((x,y,z)=\)\((3,0,0)\) または \((0,3,0)\) のときであるから,
\(\left(\displaystyle\frac{3}{6}\right)^3+\left(\displaystyle\frac{2}{6}\right)^3=\displaystyle\frac{35}{216}\)
(2) サイコロを \(4\) 回振った時点で点 \(P\) が頂点 \(E\) の位置にある確率
\((x,y,z)=\)\((3,1,0)\) または \((2,0,2)\) または \((0,4,0)\) のときであるから,
\(_{4}C_{3}\left(\displaystyle\frac{3}{6}\right)^3\left(\displaystyle\frac{2}{6}\right)+_{4}C_{2}\left(\displaystyle\frac{3}{6}\right)^2\left(\displaystyle\frac{1}{6}\right)^2+\left(\displaystyle\frac{2}{6}\right)^4=\displaystyle\frac{143}{648}\)
(3) サイコロを \(6\) 回振った時点で点 \(P\) が頂点 \(A\) の位置にある確率
・\(1\) 周して点 \(P\) が頂点 \(A\) の位置にくるとき
\((x,y,z)=\)\((6,0,0)\) または \((0,6,0)\) のときであるから,
\(\left(\displaystyle\frac{3}{6}\right)^6+\left(\displaystyle\frac{2}{6}\right)^6=\displaystyle\frac{793}{6^6}\)
・\(1\) 周せずに点 \(P\) が頂点 \(A\) の位置にくるとき
\(x=y\) となればよいので,
\((x,y,z)=\)\((0,0,6)\) または \((1,1,4)\) または \((2,2,2)\) または \((3,3,0)\)のときであるから,
\(\left(\displaystyle\frac{1}{6}\right)^6+_{6}C_{1}\left(\displaystyle\frac{3}{6}\right)\times _{5}C_{1}\left(\displaystyle\frac{2}{6}\right)\left(\displaystyle\frac{1}{6}\right)^4\\+_{6}C_{2}\left(\displaystyle\frac{3}{6}\right)^2\times _{4}C_{2}\left(\displaystyle\frac{2}{6}\right)^2\left(\displaystyle\frac{1}{6}\right)^2+_{6}C_{3}\left(\displaystyle\frac{3}{6}\right)^3\left(\displaystyle\frac{2}{6}\right)^3\)
\(=\displaystyle\frac{1+180+3240+4320}{6^6}=\displaystyle\frac{7741}{6^6}\)
したがって,\(\displaystyle\frac{793+7741}{6^6}=\displaystyle\frac{8534}{6^6}=\displaystyle\frac{4267}{23328}\)







コメント