\(f(x)=2x^3-9x^2+6x\)
の極大値を \(M\) ,極小値を \(m\) とするとき,以下の値を求めよ.
① \(M+m\)
② \(M-m\)


はじめに(ただ答えが出せるだけでは✖)
\(f(x)=2x^3-9x^2+6x\) より
\(f^{\prime}(x)=6x^2-18x+6=6(x^2-3x+1)\)
\(f^{\prime}(x)=0\) より
\(x=\displaystyle\frac{3\pm\sqrt{5}}{2}\)
これを \(f(x)=2x^3-9x^2+6x\) に代入すれば当然答えは出ますが・・・・・
(もっと面倒な計算でもしますか??または文字が入っていたら・・・)
または、2021 近畿大学【数学Ⅱ・高次方程式】計算の工夫で紹介したように、
\(f(x)\) を \(f^{\prime}(x)\) で割り、その余りに代入すると言う手法もあります.
せめてガッツで計算するにしても、計算の工夫をして欲しいものです.
ここでは、3次関数の「極値の和」と「極値の差」というポイントを紹介します.
このポイントは様々な問題に応用が出来ますので、是非今回の具体的な問題でしっかりと理解し、他の問題でも使えるようにしていきましょう!
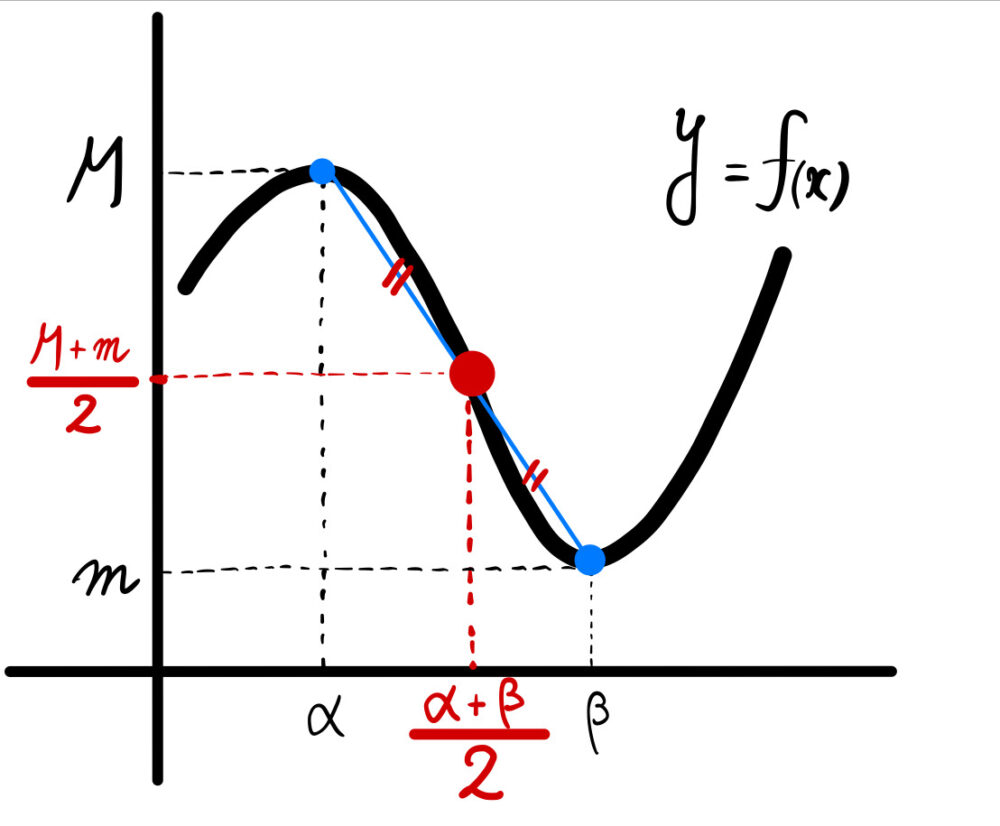
「極値の和」について
3次関数のグラフは、
極大点と極小点の中点(変曲点という)
に関して対称つまり、\(f^{\prime}(x)=0\) となる \(x=\alpha , \beta\) \(( \alpha<\beta )\) とおくと、
\(f\left(\displaystyle\frac{\alpha+\beta}{2}\right)=\displaystyle\frac{M+m}{2}\)
①解答
\(f(x)=2x^3-9x^2+6x\) より
\(f^{\prime}(x)=6x^2-18x+6=6(x^2-3x+1)\)
\(f^{\prime}(x)=0\) となる \(x=\alpha , \beta\) \(( \alpha<\beta )\) とおくと、
解と係数の関係より、\(\alpha+\beta=3\)・・・①
3次関数のグラフは、極大点と極小点の中点に関して対称であるから、
\(f\left(\displaystyle\frac{\alpha+\beta}{2}\right)=\displaystyle\frac{M+m}{2}\)・・・②
が成立する.
①を②に代入して、
\(M+m=2f\left(\displaystyle\frac{3}{2}\right)=2\left(2\cdot\displaystyle\frac{27}{8}-9\cdot\displaystyle\frac{9}{4}+6\cdot\displaystyle\frac{3}{2}\right)=-9\)
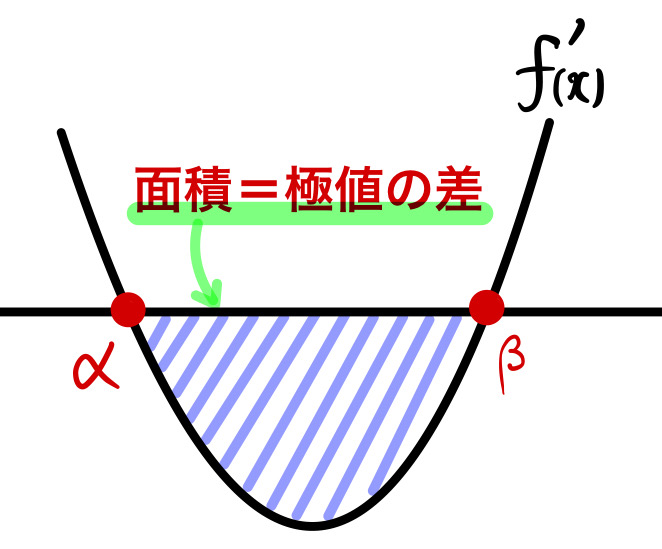
「極値の差」について
極値の差
☞ \(y=f^{\prime}(x)\) と \(x\) 軸で囲まれた面積
【Pointの説明】
上の図の面積を \(S\) とおくと、
\(S=-\displaystyle\int_{ \alpha }^{ \beta } f^{\prime}(x) dx\)
\( =-\displaystyle\left[f(x)\right]^{\beta}_{\alpha}\)
\(=f(\alpha)-f(\beta)\) (☜極値の差)
(2)解答
\(M-m=f(\alpha)-f(\beta)\)
\(=-\displaystyle\left[f(x)\right]^{\beta}_{\alpha}\)
\(=-\displaystyle\int_{ \alpha }^{ \beta } f^{\prime}(x) dx\) ・・・①
ここで、\(f^{\prime}(x)=6(x^2-3x+1)\) であり、
\(x^2-3x+1=0\) の解が \(x=\alpha , \beta\) なので、
\(f^{\prime}(x)=6(x-\alpha)(x-\beta)\)
①に代入して
\(M-m=-\displaystyle\int_{ \alpha }^{ \beta } 6(x-\alpha)(x-\beta) dx\)
\(\displaystyle\int_{ \alpha }^{ \beta } (x-\alpha)(x-\beta)=-\displaystyle\frac{1}{6}(\beta-\alpha)^3\) より
\(M-m=(\beta-\alpha)^3\)
\(=\left\{(\beta-\alpha)^2\right\}^{\frac{3}{2}}\)
\(=\left\{(\alpha+\beta)^2-4\alpha\beta\right\}^{\frac{3}{2}}\)
\(x^2-3x+1=0\) の解が \(x=\alpha , \beta\) なので、解と係数の関係から
\(\alpha+\beta=3\)、\(\alpha\beta=1\)
よって、\(M-m=\displaystyle5^{\frac{3}{2}}=5\sqrt{5}\)






コメント