【2021数学ⅡB(第2日程)】第4問(数列)
[1]問題と解答・解説《ア〜キ》
[1]解答・解説《ア〜キ》

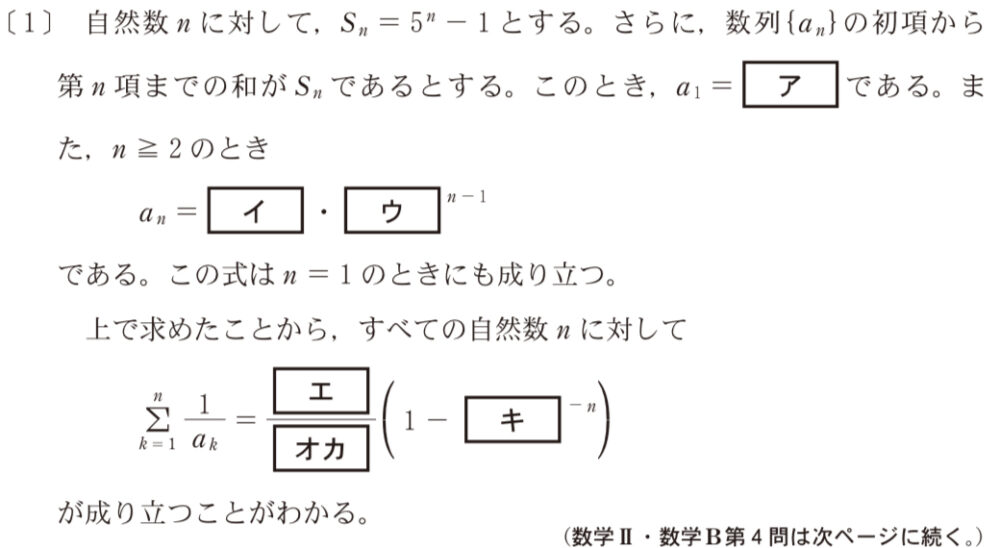
\(S_{n}\) と \(a_{n}\) の関係について
① \(a_{1}=S_{1}\)
② \(a_{n}=S_{n}-S_{n-1}\) ( \(n≧2\) )
\(a_{1}=S_{1}=5^1-1=4\) ・・・《ア》
また,\(n≧2\) のとき
\(a_{n}=S_{n}-S_{n-1}\) より
\(a_{n}=(5^n-1)-(5^{n-1}-1)=5\cdot 5^{n-1}-5^{n-1}\)
よって,\(a_{n}=4\cdot 5^{n-1}\) ・・・《イウ》
これは \(n=1\) のときも成り立つ.
よってすべての自然数 \(n\) に対して,
\(\displaystyle\frac{1}{a_{n}}=\displaystyle\frac{1}{4}\cdot\left(\displaystyle\frac{1}{5}\right)^{n-1}\) であるから,
数列 \(\left\{\displaystyle\frac{1}{a_{n}}\right\}\) は初項 \(\displaystyle\frac{1}{4}\) ,公比 \(\displaystyle\frac{1}{5}\) の等比数列となる
したがって,
\(\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{1}{a_{k}}}=\displaystyle\frac{\displaystyle\frac{1}{4}\left\{1-\left(\displaystyle\frac{1}{5}\right)^n\right\}}{1-\displaystyle\frac{1}{5}}\)
\(=\displaystyle\frac{5}{16}(1-5^{-n})\) ・・・《エ〜キ》
[2](1)問題と解答・解説《ク〜セ》
[2](1)解答・解説《ク〜セ》
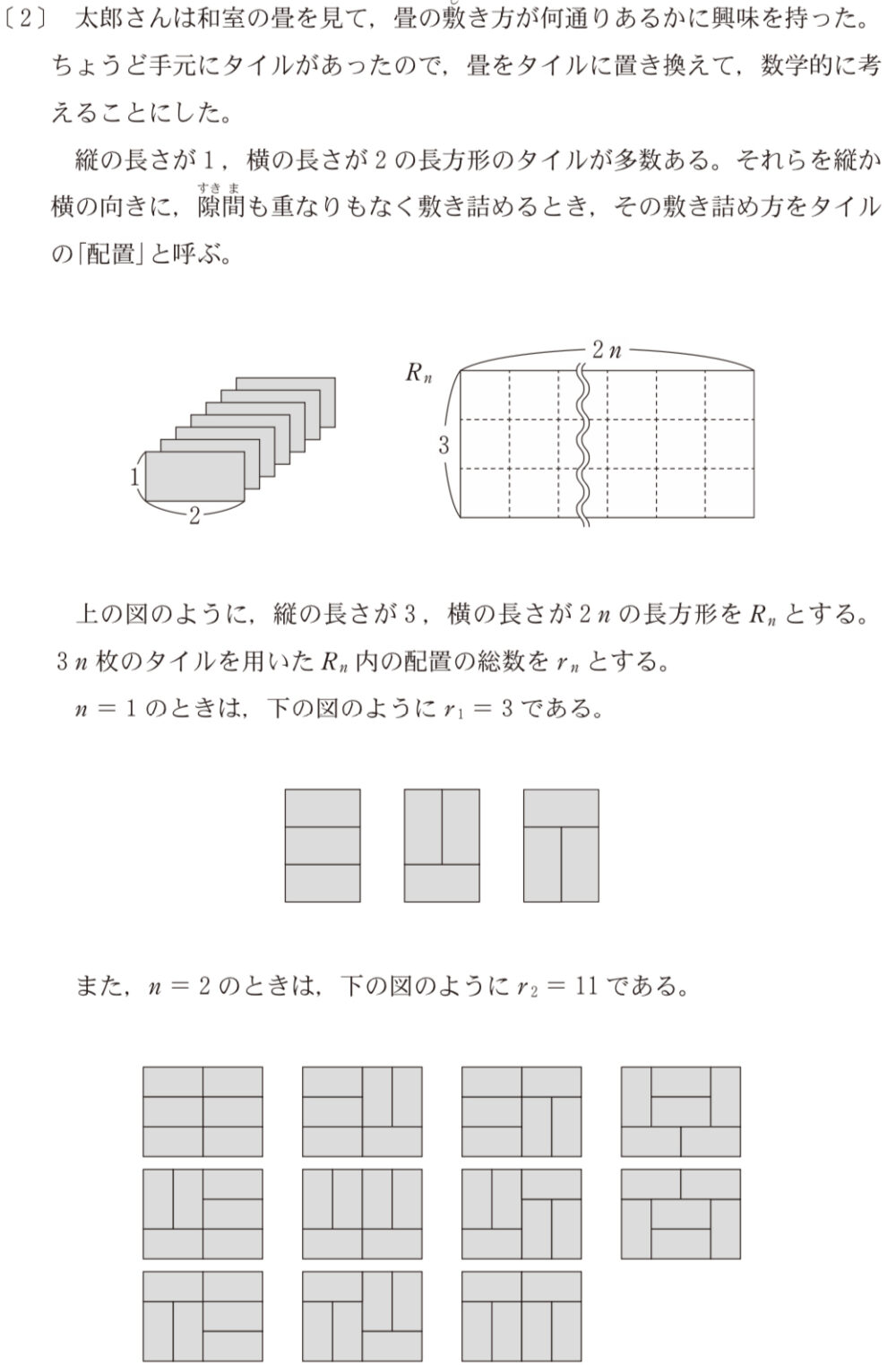
\(n=1\) のとき
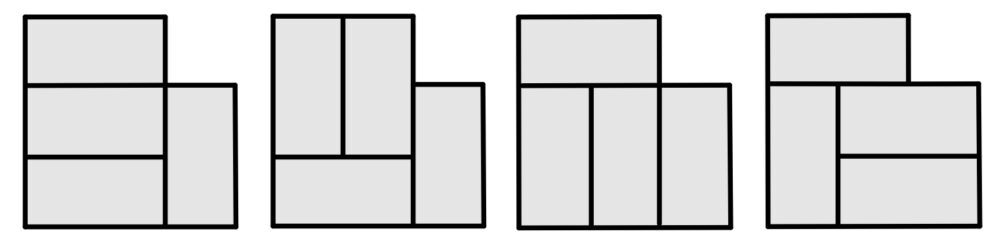
の \(4\) 通りある.よって,\(t_{1}=4\) ・・・《ク》
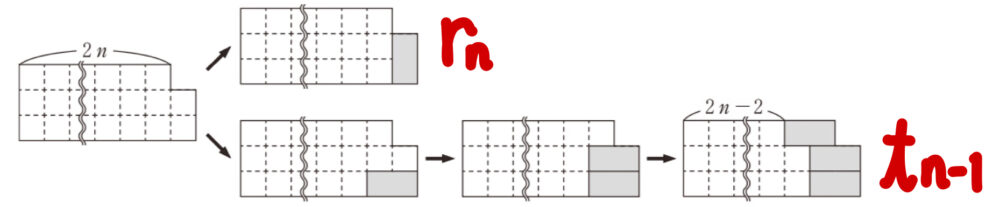
この図から,\(2\) 以上の自然数 \(n\) に対して
\(t_{n}=r_{n}+t_{n-1}\) が成り立つ.
よって,\(A=1\) ,\(B=1\) ・・・《ケコ》
以上から,\(t_{2}=r_{2}+t_{1}=11+4=\) \(15\) ・・・《サシ》
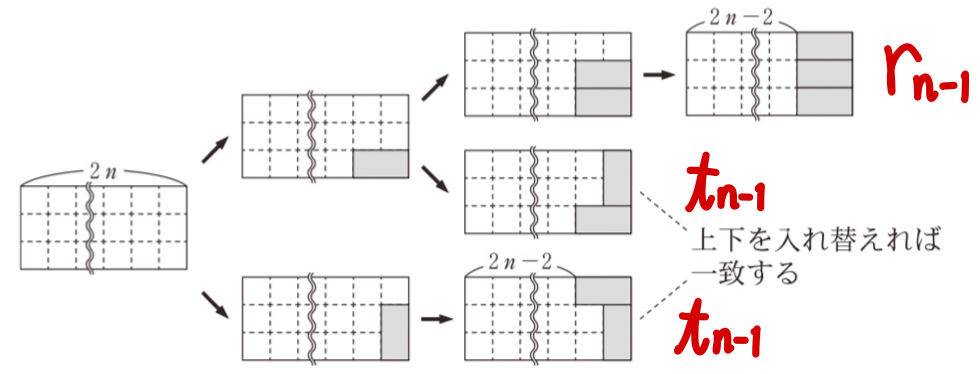
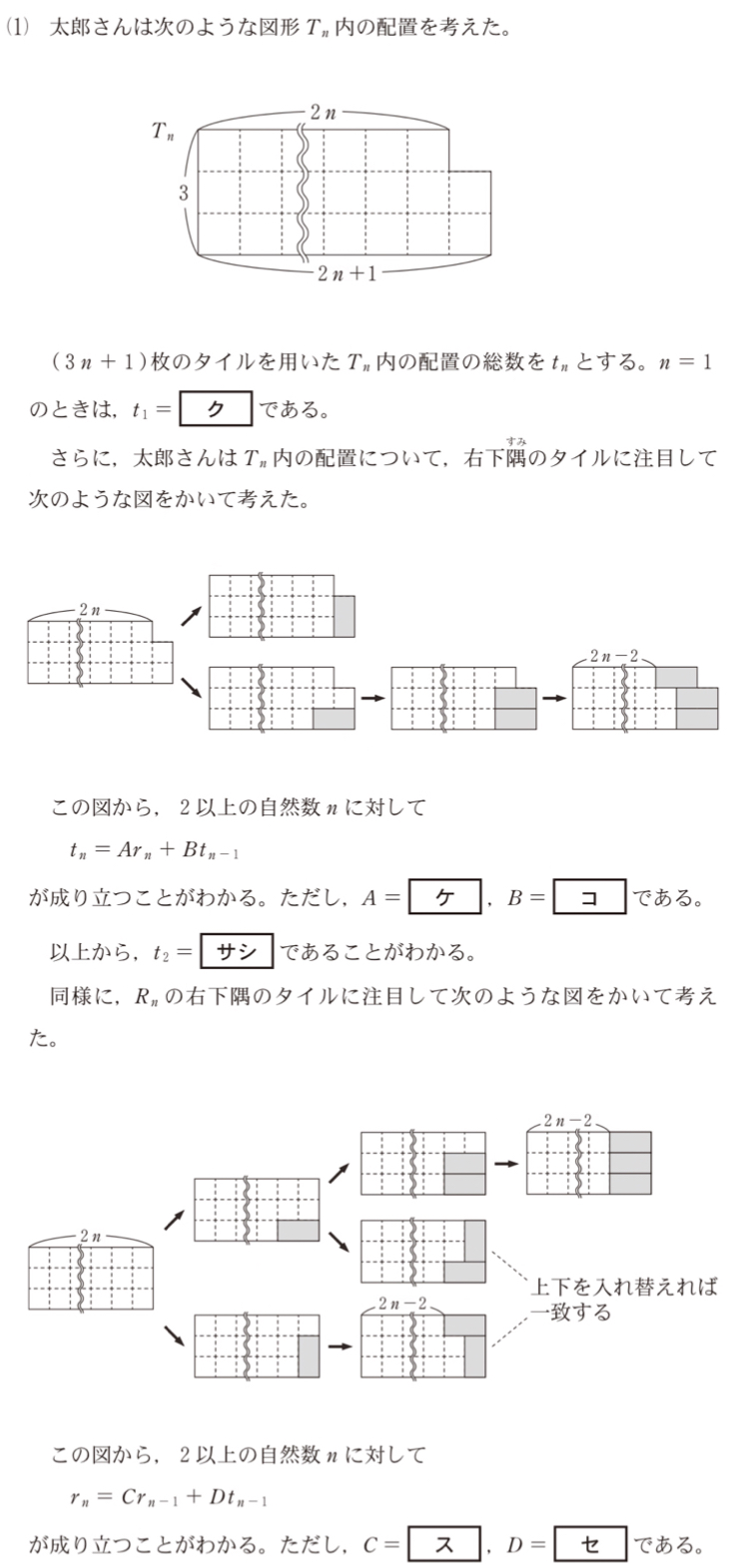
同様にこの図から,\(2\) 以上の自然数 \(n\) に対して
\(r_{n}=r_{n-1}+t_{n-1}+t_{n-1}=r_{n-1}+2t_{n-1}\) が成り立つ.
よって,\(C=1\) ,\(D=2\) ・・・《スセ》
[2](2)問題と解答・解説《ソ〜テ》

[2](2)解答・解説《ソ〜テ》
畳を縦の長さが \(1\) ,横の長さが \(2\) の長方形とみなす.
縦の長さが \(3\) ,横の長さが \(6\) の長方形の部屋に畳を敷き詰めるとき,その総数は
\(r_{3}=r_{2}+2t_{2}=11+2\times 15=\)\(41\) ・・・《ソタ》
縦の長さが \(3\) ,横の長さが \(8\) の長方形の部屋に畳を敷き詰めるとき,その総数は
\(r_{4}=r_{3}+2t_{3}=r_{3}+2(r_{3}+t_{2})=3r_{3}+2t_{2}\)
\(=3\times 41+2\times 15=\)\(153\) ・・・《チツテ》







コメント