【滋賀医科大学】
\(AB=3\)、\(BC=4\)、\(CA=5\) である \(\triangle ABC \) において、\(\angle{C}=\theta\) とする.
次を示せ.
(1) \(30\text{°}<\theta\)
(2) \(\theta<40\text{°}\)
(3) \(36\text{°}<\theta\)
(4) \(n\theta=30\text{°}+m\times 360\text{°}\) となる整数 \(m , n\) は存在しない.
![]()
考え方
(1)について
\(\triangle ABC \) は、\(3\) 辺の長さが「\(3\)、\(4\)、\(5\)」の有名直角三角形
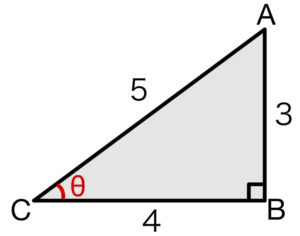
※\(3\) 辺の長さが「\(5\)、\(12\)、\(13\)」も有名直角三角形であるので覚えておこう!

また、下図(\(y=\cos x\) のグラフ)を見て下さい.
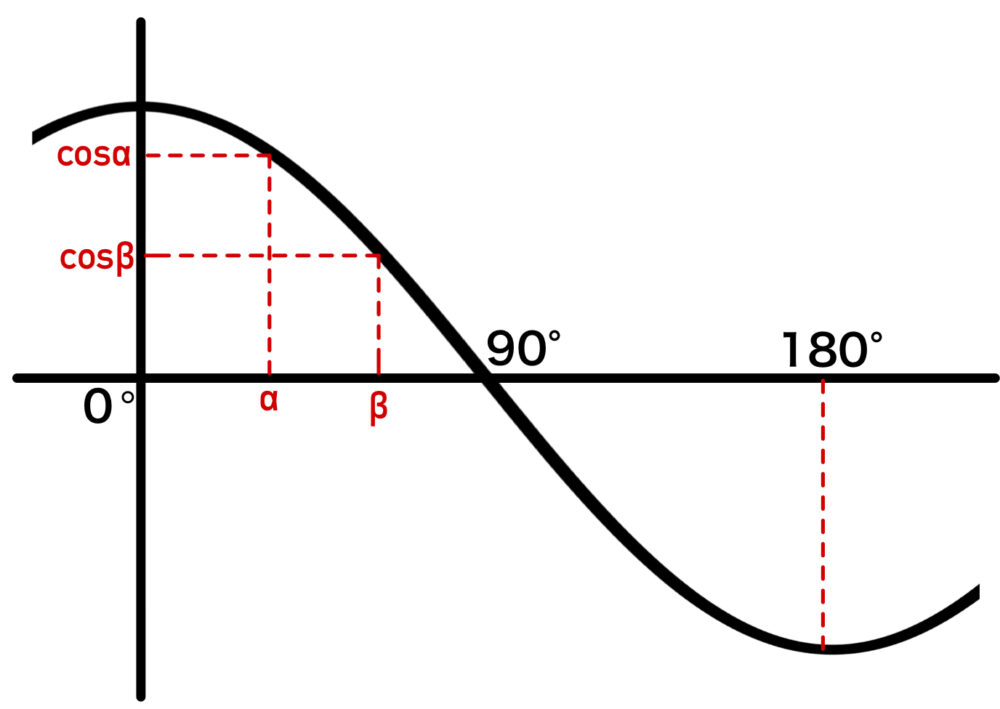
\(y=\cos x\) のグラフは、\(0\text{°}<\theta<180\text{°}\) の範囲において、
\(\alpha<\beta\) \(\iff\) \(\cos\alpha>\cos\beta \)
(※大小関係が入れ替わる)
このような関数のことを、減少関数という.
(2)について
【\(3\) 倍角の公式の利用】
\(\cos 3\theta =4\cos^3\theta -3\cos \theta \)
\(40\text{°}\) においては、
\(\sin 40\text{°}\) や \(\cos 40\text{°}\) の値を計算することは困難.
そこで、\(40\text{°}\times 3=120\text{°}\) を考える
つまり、\(3\) 倍角の公式を利用する!!
(3)について
\(36\text{°}\) は有名角!!
【cos36°】解法2種類(倍角の公式利用)と(二等辺三角形で余弦定理)
にまとめています.頻出ですから、誘導なしで求められるようにしておきましょう!
(4)について
「〇〇しないをしめせ」と言われたとき、1つの方法として、背理法「〇〇する」と仮定からスタート!
\(2\) 段仮定の数学的帰納法の利用
\(2\) 段仮定の数学的帰納法については、有名問題として

で扱っています.知っているかどうかで差がつく頻出重要問題ですので、しっかりと演習を!
![]()
【滋賀医科大学】
\(AB=3\)、\(BC=4\)、\(CA=5\) である \(\triangle ABC \) において、\(\angle{C}=\theta\) とする.
次を示せ.
(1) \(30\text{°}<\theta\)
(2) \(\theta<40\text{°}\)
(3) \(36\text{°}<\theta\)
(4) \(n\theta=30\text{°}+m\times 360\text{°}\) となる整数 \(m , n\) は存在しない.
解答(1)〜(3)
(1) \(AB^2+BC^2=3^2+4^2=5^2=CA^2\) が成立(三平方の定理の逆)するので、\(\angle{B}=90\text{°}\).
よって、\(\sin\theta=\displaystyle\frac{3}{5}\)、\(\cos\theta=\displaystyle\frac{4}{5}\) ・・・①
ここで、\(\cos 30\text{°}=\displaystyle\frac{\sqrt{3}}{2}\)、\(\cos 45\text{°}=\displaystyle\frac{\sqrt{2}}{2}\) で、
\(\displaystyle\frac{\sqrt{2}}{2}<\displaystyle\frac{4}{5}<\displaystyle\frac{\sqrt{3}}{2}\)
つまり、\(\cos 45\text{°}<\cos\theta<\cos 30\text{°}\)
\(0\text{°}<x<180\text{°}\) で \(y=cos x\) は減少関数であるから、
\(30\text{°}<\theta<45\text{°}\) ・・・②
したがって、\(30\text{°}<\theta\)
(2) \(\cos 3\theta =4\cos^3\theta -3\cos \theta \) ・・・③
①より \(\cos\theta=\displaystyle\frac{4}{5}\) であるから、
③に代入して計算すると、
\(\cos 3\theta=-\displaystyle\frac{44}{125}\)
\(\cos 3\times 40\text{°}=\cos 120\text{°}-\displaystyle\frac{1}{2}<-\displaystyle\frac{44}{125}\)
つまり、\(\cos120\text{°}<\cos 3\theta \)
②より、\(90\text{°}<3\theta<135\text{°}\) より
\(0\text{°}<x<180\text{°}\) で \(y=cos x\) は減少関数であるから、
\(120\text{°}>3\theta\)
よって、\(\theta<40\text{°}\)
(3) 「【cos36°】解法2種類(倍角の公式利用)と(二等辺三角形で余弦定理)」を参考に
\(\cos 36\text{°}=\displaystyle\frac{1+\sqrt{5}}{4}>\displaystyle\frac{4}{5}=\cos \theta\)
\(0\text{°}<x<180\text{°}\) で \(y=cos x\) は減少関数であるから、
\(36\text{°}<\theta\)
(4) 考え方と解答
(4)考え方[より詳しく]
\(\cos n\theta\) が有理数になることが言えれば、④より矛盾であることが導ける
☆方針☆
すべての整数 \(n\) に対して、\(\cos n\theta\) が有理数を示せば良い
(4)解答
さいごに
いかがだったでしょうか?(4)については、さすが医学部の問題といった難問です。
しかし(1)〜(3)は、医学部志望以外の人も、絶対に落としてはいけない問題です。
そして(4)については、確かに難しいですが、考え方を学ぶ上では、とても良い問題だと思います。
最後まで解けなくても、考え方・方針の立て方をしっかりと勉強し、初見の問題にも対応できる力を身につけていきましょう!








コメント