【2023東京大学・文科・第２問】絶対値を含む定積分の最大値・最小値

解答・解説

(１)　\(-1≦a≦2\) のとき \(g(a)=\displaystyle\int^{a}_{-1}f(t) dt\)

点 \(P(t,3t^2-4t)\) と \(l\)：\(2x-y=0\) の距離は

\(f(t)=\displaystyle\frac{|2t-(3t^2-4t)|}{\sqrt{2^2+(-1)^2}}=\displaystyle\frac{1}{\sqrt{5}|3t^2-6t|}\)

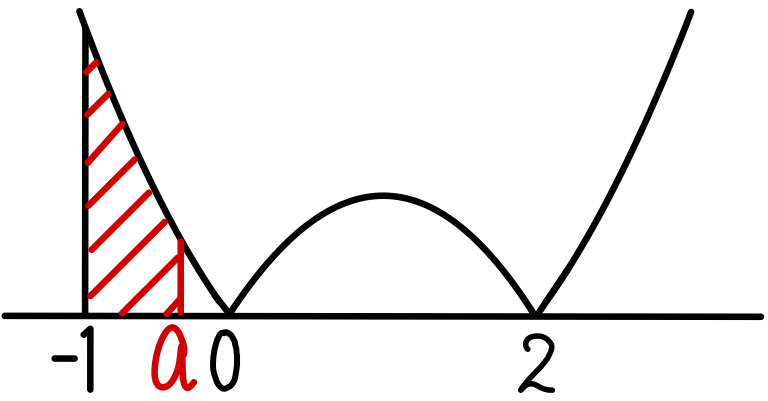( ⅰ )　\(-1≦a≦0\) のとき

\(g(a)=\displaystyle\frac{1}{\sqrt{5}}\displaystyle\int^{a}_{-1}(3t^2-6t) dt\)

\(=\displaystyle\frac{1}{\sqrt{5}}\Bigl[t^3-3t^2\Bigr]^{a}_{-1}\)

\(=\displaystyle\frac{1}{\sqrt{5}}(a^3-3a^2+4)\)

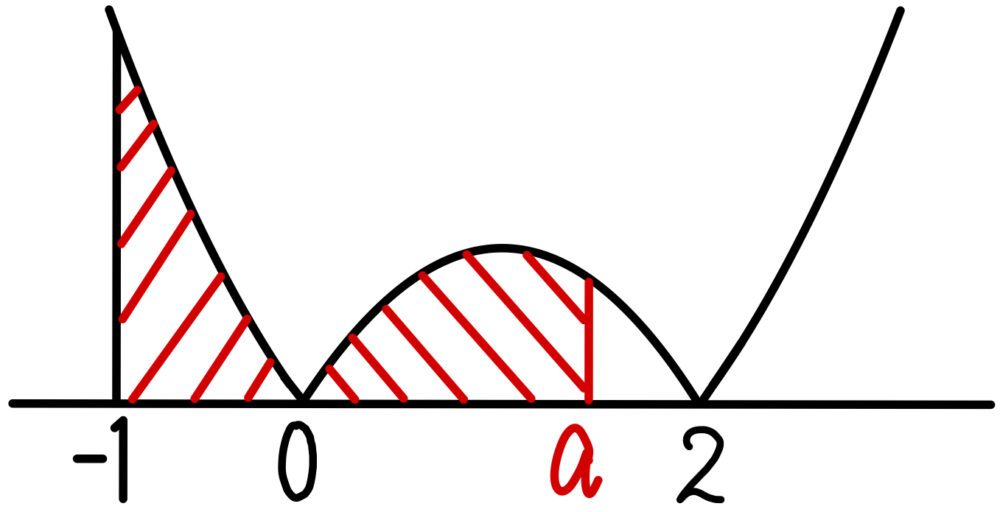( ⅱ )　\(0≦a≦2\) のとき

\(g(a)=\displaystyle\frac{1}{\sqrt{5}}\left\{\displaystyle\int^{0}_{-1} (3t^2-6t)dt+\displaystyle\int^{a}_{0}(-3t^2+6t) dx\right\}\)

\(=\displaystyle\frac{1}{\sqrt{3}}\left\{\Bigl[t^3-3t^2\Bigr]^{0}_{-1}+\Bigl[-t^3+3t^2\Bigr]^{a}_{0}\right\}\)

\(=\displaystyle\frac{1}{\sqrt{5}}(-a^3+3a^2+4)\)

したがって，

\(-1≦a≦0\) のとき

\(g(a)=\displaystyle\frac{1}{\sqrt{5}}(a^3-3a^2+4)\)

\(0≦a≦2\) のとき

\(g(a)=\displaystyle\frac{1}{\sqrt{5}}(-a^3+3a^2+4)\)

(２)　\(0≦a≦2\) のとき，\(g(a)-f(a)\) の最大値および最小値

\(f(a)=\displaystyle\frac{1}{\sqrt{5}}|3a^2-6a|\) で

\(0≦a≦2\) のとき \(3a^2-6a=3a(a-2)≦0\) より

\(f(a)=\displaystyle\frac{1}{\sqrt{5}}(-3a^2+6a)\)

また(１)より，

\(0≦a≦2\) のとき

\(g(a)=\displaystyle\frac{1}{\sqrt{5}}(-a^3+3a^2+4)\)

よって，

\(g(a)-f(a)=\displaystyle\frac{1}{\sqrt{5}}\left\{(-a^3+3a^2+4)-(-3a^2+6a)\right\}\)

\(=\displaystyle\frac{1}{\sqrt{5}}(-a^3+6a^2-6a+4)\)

ここで，\(h(a)=-a^3+6a^2-6a+4\) とおくと

\(h^{\prime}(a)=-3a^2+12a-6=-3(a^2-4a+2)\)

\(h^{\prime}(a)=0\) のとき \(a=2\pm\sqrt{2}\) より

\(0≦a≦2\) における増減表は次のとおり

\(h(a)=(-a+2)(a^2-4a+2)+4a\) より

\(h(2-\sqrt{2})=4(2-\sqrt{2})\)

したがって，

\(a=2\) のとき最大値：\(\displaystyle\frac{8}{\sqrt{5}}=\displaystyle\frac{8\sqrt{5}}{5}\)

\(a=2-\sqrt{2}\) のとき最小値：\(\displaystyle\frac{4(2-\sqrt{2})}{\sqrt{5}}=\displaystyle\frac{4\sqrt{5}}{5}(2-\sqrt{2})\)

【2023東京大学・文科・第３問】同じものを含む順列、条件付き確率

黒玉3個、赤玉4個、白玉5個を横一列に並べる。どの赤玉も隣り合わない確率。どの赤玉も隣り合わないとき、どの黒玉も隣り合わない条件付き確率。2023東大・文系。解答・解説。過去問題演習対策。数学A：場合の数、確率

mathmathmanabu.com

2023.03.09