【問題8】(1970上智大学)
\(3\) つの複素数 \(\alpha\)、\(\beta\)、\(\gamma\) の間に、関係式 \(| \alpha |=| \beta |=| \gamma |=1\)、\(\alpha+\beta+\gamma=0\) が成り立つならば、複素数平面上で \(\alpha\)、\(\beta\)、\(\gamma\) を \(3\) 頂点とする三角形は [ ] である.
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
考え方・方針の立て方
\(O ( 0 )\)、\(A ( \alpha )\)、\(B ( \beta )\)、\(C ( \gamma )\) とし、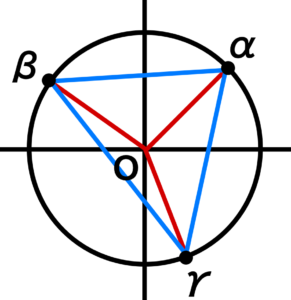
\(| \alpha |=| \beta |=| \gamma |=1\) ・・・①
\(\alpha+\beta+\gamma=0\) ・・・② とおく.
このとき、
①より、\(3\) つの複素数 \(\alpha\)、\(\beta\)、\(\gamma\) は、中心 \(O\) 、半径 \(1\) の円上にある
②より、\(\displaystyle\frac{\alpha+\beta+\gamma}{3}=0\) なので、\(△ABC\) の重心は \(O\)
つまり、\(O\) は \(△ABC\) の「外心」かつ「重心」
☞ 外心と重心が一致する三角形は正三角形
もちろん、「外心と重心が一致する三角形は正三角形」であることを証明しても良いが、ここでは複素数を使った解答で考えると、
原点を中心に \(\alpha\) を \(\pm\displaystyle\frac{2}{3}\pi\) 回転した点が \(\beta\)、
原点を中心に \(\alpha\) を \(\mp\displaystyle\frac{2}{3}\pi\) 回転した点が \(\gamma\) になること、
つまり、次の(Ⅰ)かつ(Ⅱ)を示せばよい.
(Ⅰ) \(\displaystyle\frac{\beta}{\alpha}=\cos \left(\pm\displaystyle\frac{2}{3}\pi\right)+i\sin \left(\pm\displaystyle\frac{2}{3}\pi\right)\)
(Ⅱ) \(\displaystyle\frac{\gamma}{\alpha}=\cos \left(\mp\displaystyle\frac{2}{3}\pi\right)+i\sin \left(\mp\displaystyle\frac{2}{3}\pi\right)\)
そこで、(Ⅰ)の \(\displaystyle\frac{\beta}{\alpha}\) を求めるためには、①、②から \(\gamma\) を消去する必要がある.
つまり、②から \(\gamma=-(\alpha+\beta)\) として、①の \(| \gamma |=1\) に代入!
解答
\(O ( 0 )\)、\(A ( \alpha )\)、\(B ( \beta )\)、\(C ( \gamma )\) とし、
\(| \alpha |=| \beta |=| \gamma |=1\) ・・・①
\(\alpha+\beta+\gamma=0\) ・・・② とおく.
②より \(\gamma=-(\alpha+\beta)\) を、①の \(| \gamma |=1\) に代入すると、
\(| \alpha+\beta |=1\)
\(2\) 乗すると、
\(| \alpha+\beta |^2=1 \iff (\alpha+\beta)(\overline{\alpha}+\overline{\beta})=1\)
\(\alpha\overline{\alpha}+\alpha\overline{\beta}+\overline{\alpha}\beta+\beta\overline{\beta}=1\)
\(| \alpha |=1 \iff \alpha\overline{\alpha}=1 \iff \overline{\alpha}=\displaystyle\frac{1}{\alpha}\)、
\(| \beta |=1 \iff \beta\overline{\beta}=1 \iff \overline{\beta}=\displaystyle\frac{1}{\beta}\) なので
\(\displaystyle\frac{\alpha}{\beta}+\displaystyle\frac{\beta}{\alpha}+1=0\)
この上の式に \(\displaystyle\frac{\beta}{\alpha}\) をかけると、
\(\left(\displaystyle\frac{\beta}{\alpha}\right)^2+\displaystyle\frac{\beta}{\alpha}+1=0\)
よって、
\(\displaystyle\frac{\beta}{\alpha}=\displaystyle\frac{-1\pm\sqrt{3}i}{2}=\cos \left(\pm\displaystyle\frac{2}{3}\pi\right)+i\sin \left(\pm\displaystyle\frac{2}{3}\pi\right)\)
また、②より \(\gamma=-(\alpha+\beta)\) を \(\alpha\) で割って、
\(\displaystyle\frac{\gamma}{\alpha}=-1-\displaystyle\frac{\beta}{\alpha}=\displaystyle\frac{-1\mp\sqrt{3}i}{2}=\cos \left(\mp\displaystyle\frac{2}{3}\pi\right)+i\sin \left(\mp\displaystyle\frac{2}{3}\pi\right)\)
したがって、複素数平面上で \(\alpha\)、\(\beta\)、\(\gamma\) を \(3\) 頂点とする三角形は [ 正三角形 ] である.









コメント