【問題9】(1967 一橋大学)
平面上ではじめに座標の原点にあった動点 \(P\) が、\(x\) 軸の正方向に \(1\) だけ進む.
次に進行方向に向かって左へ \(30°\) だけ向きを変えて、\(\displaystyle\frac{1}{2}\) だけ進む.
次に進行方向に向かって左へ \(30°\) だけ向きを変えて、\(\displaystyle\frac{1}{4}\) だけ進む.
以下同じように、進行方向を左へ \(30°\) ずつ変え、進む距離を前回の半分にしていくとき、動点 \(P\) の極限値の位置を求めよ.
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
考え方・確認事項
方針:複素数の回転の利用
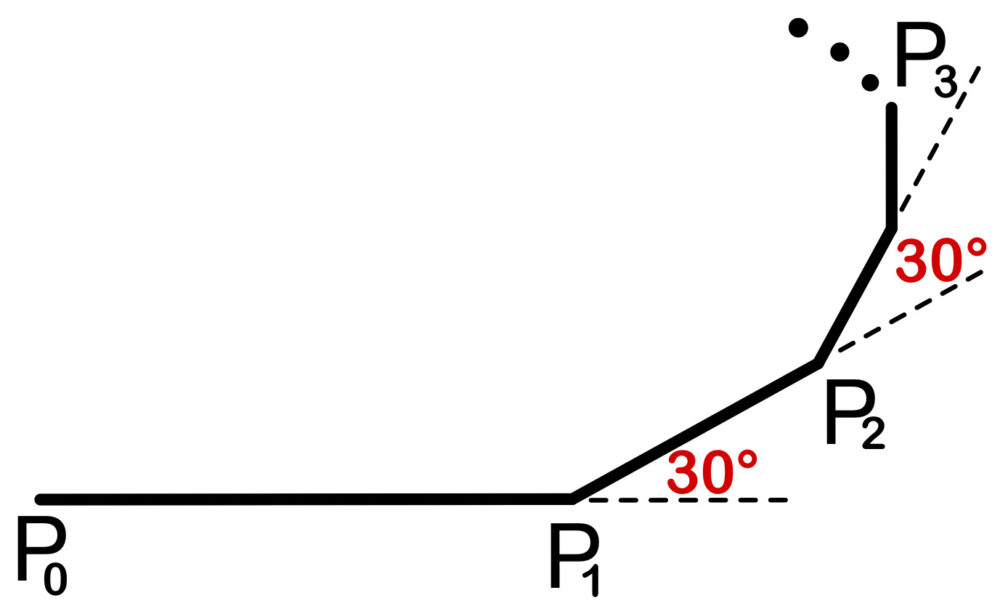
\(xy\) 平面で原点を \(P_{0}\) とし、動点 \(P\) が \(n\) 回移動した後の点を \(P_{n}\) とする.また、\(P_{n}\) を表す複素数を \(z_{n}\) とする.
\(\overrightarrow{P_{n-1}P_{n}}\) を \(\displaystyle\frac{1}{2}\) 倍して、\(30°\) 回転したものが \(\overrightarrow{P_{n}P_{n+1}}\) より
\(\alpha=\displaystyle\frac{1}{2}(\cos 30°+i\sin 30°)=\displaystyle\frac{1}{4}(\sqrt{3}+i)\) とおくと、
\(z_{n+1}-z_{n}=\alpha(z_{n}-z_{n-1})\) という関係式が成り立つ.
三項間漸化式と特性方程式
三項間漸化式 \(a_{n+2}+pa_{n+1}+qa_{n}=0\)
の特性方程式 \(x^2+px+q=0\)
を解いた解が \(x=\alpha , \beta\) のとき
\(a_{n+2}+pa_{n+1}+qa_{n}=0\\ \iff \begin{cases} a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_{n})\\a_{n+2}-\beta a_{n+1}=\alpha(a_{n+1}-\beta a_{n}) \end{cases}\)
解答
\(xy\) 平面で原点を \(P_{0}\) とし、動点 \(P\) が \(n\) 回移動した後の点を \(P_{n}\) とする.また、\(P_{n}\) を表す複素数を \(z_{n}\) とする.
このとき、\(P_{0}( 0 , 0 )\)、\(P_{1}( 1 , 0 )\) より、
\(z_{0}=0\)、\(z_{1}=1\)
また自然数 \(n\) に対して
\(\overrightarrow{P_{n-1}P_{n}}\) を \(\displaystyle\frac{1}{2}\) 倍して、\(30°\) 回転したものが \(\overrightarrow{P_{n}P_{n+1}}\) より
\(\alpha=\displaystyle\frac{1}{2}(\cos 30°+i\sin 30°)=\displaystyle\frac{1}{4}(\sqrt{3}+i)\) とおくと、
\(z_{n+1}-z_{n}=\alpha(z_{n}-z_{n-1})\) ・・・①
三項間漸化式の特性方程式を解く(この部分は解答には残しません)
\(x^2-x=\alpha(x-1)\)
\(x^2-(\alpha+1)x+\alpha=0\)
\((x-1)(x-\alpha)=0\)
\(x=1 , \alpha\)
①を変形すると
\(z_{n+1}-\alpha z_{n}=z_{n}-\alpha z_{n-1}\) ・・・②
①より、
\(z_{n+1}-z_{n}=(z_{1}-z_{0})\alpha^n\)
よって、\(z_{n+1}-z_{n}=\alpha^n\) ・・・③
②より、
\(z_{n+1}-\alpha z_{n}=(z_{1}-\alpha z_{0})\cdot 1^n\)
よって、\(z_{n+1}-z_{n}=1\) ・・・④
③-④より、\((\alpha-1)z_{n}=\alpha^n-1\)
\(\alpha\not=1\) より \(\displaystyle\frac{1-\alpha^n}{1-\alpha}\)
ここで、\(| \alpha |=\displaystyle\frac{1}{2}\) より
\(\displaystyle\lim_{n\rightarrow\infty}|\alpha^n|=\displaystyle\lim_{n\rightarrow\infty}\alpha^n=0 \)
したがって、\(\displaystyle\lim_{n\rightarrow\infty}z_{n}=\displaystyle\frac{1}{1-\alpha}\)
\(\alpha=\displaystyle\frac{1}{4}(\sqrt{3}+i)\) を代入して式をまとめると、
\(\displaystyle\lim_{n\rightarrow\infty}z_{n}=\displaystyle\frac{1}{13}\left\{(14+3\sqrt{3})+i(5+2\sqrt{3})\right\}\)
以上より、求める点 \(P\) は
\(P \left( \displaystyle\frac{14+3\sqrt{3}}{13} , \displaystyle\frac{5+2\sqrt{3}}{13}\right)\)









コメント