【問題7】(2004横浜国立大学)
異なる複素数 \(\alpha\)、 \(\beta\)、\(\gamma\) が、\(2\alpha^2+\beta^2+\gamma^2-2\alpha\beta-2\alpha\gamma=0\) を満たすとき、次の問に答えよ.
(1) \(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}\) の値を求めよ.
(2) 複素数平面上で、\(3\) 点 \(A(\alpha)\)、\(B(\beta)\)、\(C(\gamma)\) を頂点とする \(△ABC\) はどのような三角形か.
(3) \(\alpha\)、 \(\beta\)、\(\gamma\) が \(x\) の \(3\) 次方程式 \(x^3+kx+20=0\) ( \(k\) は実数の定数) の解であるとき、\(\alpha\)、 \(\beta\)、\(\gamma\) および \(k\) の値を求めよ.
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
考え方(複素数における回転について)
原点を中心とする回転

一般の点を中心とする回転
点 \(\alpha\) を中心に、点 \(\beta\) を \(k\) 倍して、角 \(\theta\) だけ回転した点が \(\gamma\) のとき
\(\gamma-\alpha=k(\cos \theta+i \sin \theta) (\beta-\alpha)\)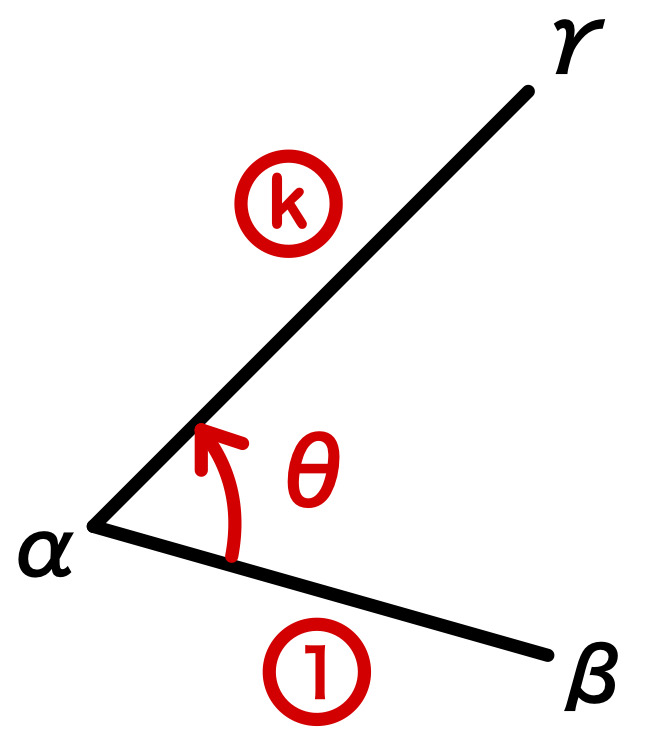
または
\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=k(\cos \theta+i \sin \theta)\)
解答
(1) \(2\alpha^2+\beta^2+\gamma^2-2\alpha\beta-2\alpha\gamma=0\) より
\(2\alpha^2=\alpha^2+\alpha^2\) と考えて
\((\alpha^2-2\alpha\beta+\beta^2)+(\gamma^2-2\alpha\gamma+\alpha^2)=0\) より
よって、\((\beta-\alpha)^2+(\gamma-\alpha)^2=0\)
\(\alpha\not=\beta\) なので、
\(\left(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}\right)^2=-1\)
したがって、\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\pm i\)
(2) (1)より、\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\cos \left(\pm\displaystyle\frac{\pi}{2}\right)+i\sin \left(\pm\displaystyle\frac{\pi}{2}\right)\) なので
\(\left|\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}\right|=1\)、\(arg \displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\pm\displaystyle\frac{\pi}{2}\)
よって、\(\gamma\) は \(\alpha\) を中心に \(\beta\) を( \(1\) 倍して、)\(\pm\displaystyle\frac{\pi}{2}\) 回転した点となる.
したがって、\(△ABC\) は、\(∠A=\displaystyle\frac{\pi}{2}\) の直角二等辺三角形
(3)
ゆえに、









コメント