【2022慶應義塾大学・理工学】
\(n\) を奇数とする. \(n\) と \(\left[\displaystyle\frac{3n+2}{2}\right]\) の積が \(6\) の倍数であるための必要十分条件を求めよ.
ただし、実数 \(x\) に対し \(x\) を超えない最大の整数を \([ x ]\) と表す.
考え方・方針の立て方
パッと見て方針が掴めない場合、まずは手を動か(実験)しましょう!
その実験を通して、規則や法則を見つけていくことを意識しましょう!
実験
・\(n=1\) のとき
\(n\times \left[\displaystyle\frac{3n+2}{2}\right]=1\times \left[\displaystyle\frac{5}{2}\right]=2\)
・\(n=3\) のとき
\(n\times \left[\displaystyle\frac{3n+2}{2}\right]=3\times \left[\displaystyle\frac{11}{2}\right]=15\)
・\(n=5\) のとき
\(n\times \left[\displaystyle\frac{3n+2}{2}\right]=5\times \left[\displaystyle\frac{17}{2}\right]=40\)
・\(n=7\) のとき
\(n\times \left[\displaystyle\frac{3n+2}{2}\right]=7\times \left[\displaystyle\frac{23}{2}\right]=77\)
・\(n=9\) のとき
\(n\times \left[\displaystyle\frac{3n+2}{2}\right]=9\times \left[\displaystyle\frac{29}{2}\right]=126\)
したがって、\(n=9\) のとき \(6\) の倍数になることが確認できました!
この実験から分かったことを下記の表にまとめてみます。
ちなみに本問では \(6\) の倍数であることを考えるため、 \(2\) の倍数と \(3\) の倍数にも注目していきます。
また、\(n\) は奇数であるので、自然数 \(m\) を用いて、 \(n=2m-1\) とする.
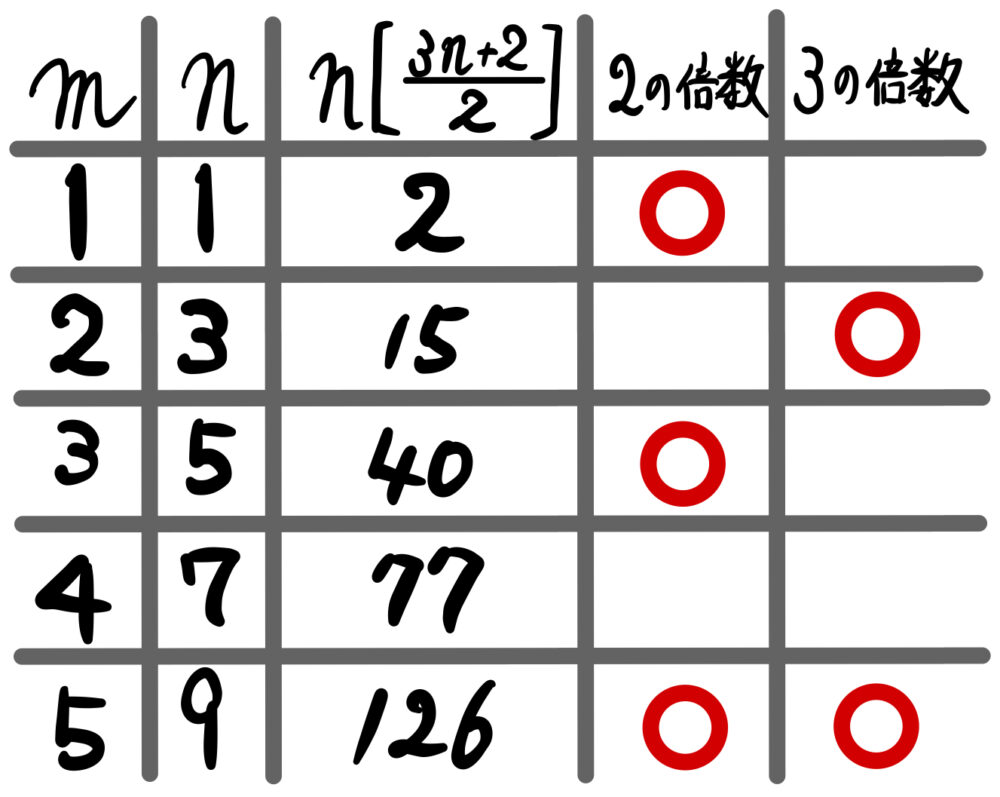
この結果より、予想できること!
\(m\) が奇数のときに \(n\times \left[\displaystyle\frac{3n+2}{2}\right]\) は \(2\) の倍数.
\(m\) が \(3\) で割って \(2\) 余る数のときに \(n\times \left[\displaystyle\frac{3n+2}{2}\right]\) は \(3\) の倍数.
👉 \(m=6k-1\) のときに \(n\times \left[\displaystyle\frac{3n+2}{2}\right]\) は \(6\) の倍数
つまり、\(n=2(6k-1)-1=12(k-1)+9\) より、\(12\) で割って \(9\) 余る数のときに条件を満たすと予想できる!
ちなみに慶應義塾大学の入試問題の場合、答えのみで良いため、証明なしでこれで答えとしても問題ない!
以下ではこの予想が正しいことをしっかりとした記述用の解答として考えていく。
解答
\(n\) は奇数より、自然数 \(m\) を用いて、 \(n=2m-1\) とおく.
\(n\) は奇数より、 \(n\times \left[\displaystyle\frac{3n+2}{2}\right]\) が \(6\) の倍数になるとき、
\(\left[\displaystyle\frac{3n+2}{2}\right]\) は \(2\) の倍数である.
このとき、 \(\left[\displaystyle\frac{3n+2}{2}\right]=\left[\displaystyle\frac{6m-1}{2}\right]=\left[3m-\displaystyle\frac{1}{2}\right]=3m-1\) であるから、
\(3m-1\) が \(2\) の倍数であるためには、\(m\) は奇数でなければならない.
ここで自然数 \(l\) を用いて \(m=2l-1\) とおける.
つまり、\(n=2m-1=2(2l-1)-1=4l-3\) のとき
\(\left[\displaystyle\frac{3n+2}{2}\right]=3m-1=3(2l-1)-1=2(3l-2)\)
\(3l-2\) は \(3\) で割ると \(1\) 余るので、\(\left[\displaystyle\frac{3n+2}{2}\right]\) は \(3\) の倍数にならない.
つまり、 \(n\times \left[\displaystyle\frac{3n+2}{2}\right]\) が \(6\) の倍数になるとき、\(n\) が \(3\) の倍数でなければならない.
以上の結果より、
\(n=4l-3\) かつ \(n\) は \(3\) の倍数のとき題意を満たす.
したがって、\(n\) は\(12\) で割って \(9\) 余る数である.







コメント