【2021数学ⅠA(第２日程)】第１問[２](図形と計量)

(１)問題と解答・解説《サ〜ソ》

(１)解答・解説《サ〜ソ》

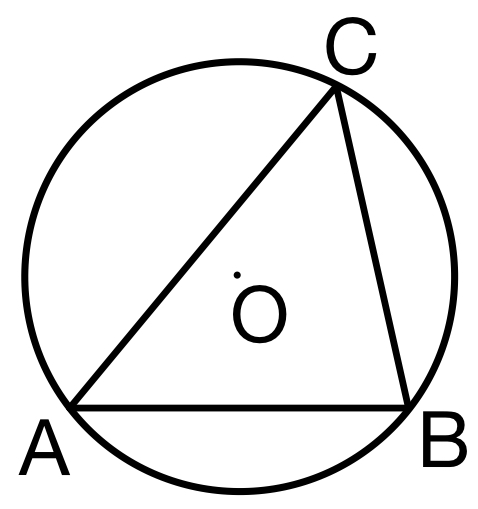 ( ⅰ )　点 \(O\) を中心とする円の半径を \(R\) とおく( \(R=5\) )

正弦定理より

\(2R=\displaystyle\frac{AB}{\sin\angle ACB}\)

\(2\times 5=\displaystyle\frac{6}{\sin\angle ACB}\)

よって，\(\sin\angle ACB=\displaystyle\frac{3}{5}\) ・・・《サ：⓪》

\(\angle ACB\) が鈍角のとき，\(\angle ACB<0\) より

\(\cos \angle ACB=-\sqrt{1-\sin^2\angle ACB}=-\sqrt{1-\left(\displaystyle\frac{3}{5}\right)^2}\)

したがって，\(\cos \angle ACB=-\displaystyle\frac{4}{5}\) ・・・《シ：⑦》

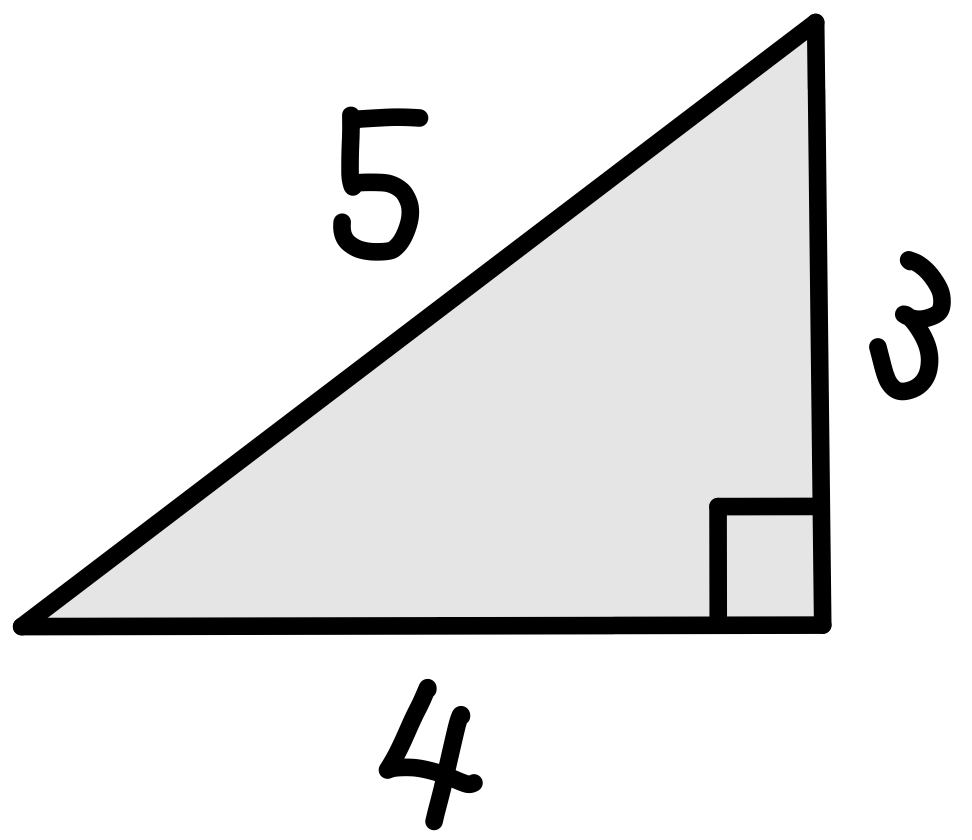\(\sin\angle ACB=\displaystyle\frac{3}{5}\) より

右図のような有名直角三角形がイメージできるようになると，いろいろと便利！

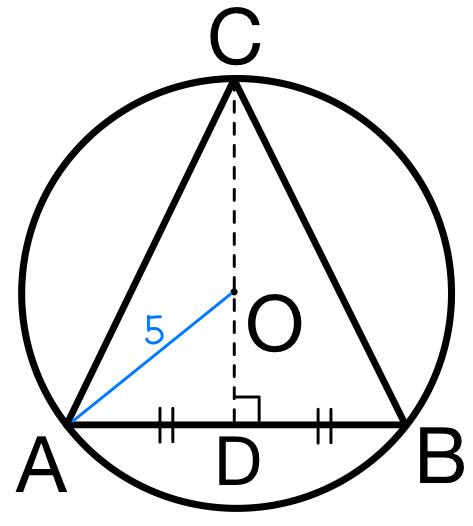( ⅱ )　\(\triangle ABC\) の面積が最大となるのは，

\(AB\) (底辺) が一定なので，\(CD\) (高さ) が最大となるときである．

つまり，右図のように点 \(O\) が線分 \(CD\) 上にあればよい．

このとき，\(\tan \angle OAD=\displaystyle\frac{OD}{AD}\) であり

\(AD=\displaystyle\frac{1}{2}AB=3\)，\(OA=R=5\) より

三平方の定理から \(OD=4\)

よって，\(\tan \angle OAD=\displaystyle\frac{4}{3}\) ・・・《ス：④》

また，\(\triangle ABC\) の面積を \(S\) とすると

\(S=\displaystyle\frac{1}{2}\cdot AB\cdot CD\) であり

\(AB=6\)，\(CD=OC+OD=5+4=9\) より

\(S=\displaystyle\frac{1}{2}\times 6\times 9=\)\(27\) ・・・《セソ》 

(２)問題と解答・解説《タ〜ハ》

(２)解答・解説《タ〜ハ》

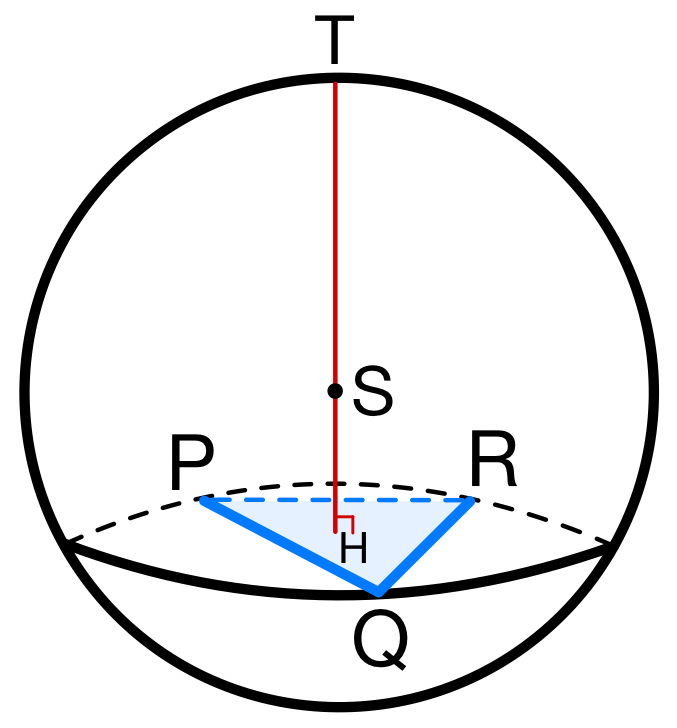
\(\triangle PQR\) で余弦定理より

\(\cos \angle QPR=\displaystyle\frac{8^2+9^2-5^2}{2\cdot 8\cdot 9}=\)\(\displaystyle\frac{5}{6}\) ・・・《タチ》 

\(\sin \angle QPR=\sqrt{1-\left(\displaystyle\frac{5}{6}\right)}=\displaystyle\frac{\sqrt{11}}{6}\) より

\(\triangle PQR=\displaystyle\frac{1}{2}\cdot 8\cdot 9\cdot \displaystyle\frac{\sqrt{11}}{6}=\)\(6\sqrt{11}\) ・・・《ツテト》 

ヘロンの公式を利用してもOKですね！

ヘロンの公式

三辺の長さが \(a\)，\(b\)，\(c\) の三角形の面積を \(S\) とすると

\(S=\sqrt{s(s-a)(s-b)(s-c)}\)

ただし，\(s=\displaystyle\frac{1}{2}(a+b+c)\)

球の中心を \(S\) とおく．

線分 \(TH\) は，球 \(S\) の中心を通る．

このとき，\(SP=SQ=SR=\)(半径)，\(SH\) は共通，\(SH\perp \triangle PQR\) より

\(\triangle SPH≡\triangle SQH≡\triangle SRH\) となる．

したがって，\(PH=QH=RH\) ・・・《ナ：⑥》

\(PH=QH=RH\) より，点 \(H\) は \(\triangle PQR\) の外心となる．

よって，\(\triangle PQR\) で正弦定理より

\(2PH=\displaystyle\frac{QR}{\sin\angle QPR}=\displaystyle\frac{5}{\displaystyle\frac{\sqrt{11}}{6}}\)

よって，\(PH=\displaystyle\frac{15}{\sqrt{11}}\)

\(\triangle SPH\) で三平方の定理から，\(SH=\displaystyle\frac{5\sqrt{2}}{\sqrt{11}}\)

以上より，求める体積は

\(\displaystyle\frac{1}{3}\times \triangle PQR\times (SH+ST)=\displaystyle\frac{1}{3}\times 6\sqrt{11}\times \left(\displaystyle\frac{5\sqrt{2}}{\sqrt{11}}+5\right)\)

\(=\) \(10(\sqrt{11}+\sqrt{2})\) ・・・《ニ〜ハ》