【2022京都大学・文】
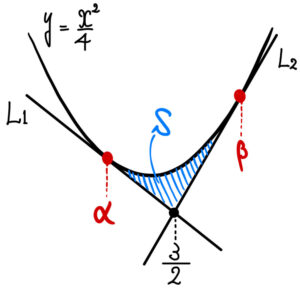
\(xy\) 平面上の \(2\) 直線 \(L_{1}\) , \(L_{2}\) は直交し,交点の \(x\) 座標は \(\displaystyle\frac{3}{2}\) である.また,\(L_{1}\) , \(L_{2}\) はともに曲線 \(C\) : \(y=\displaystyle\frac{x^2}{4}\) に接している.
このとき, \(L_{1}\) , \(L_{2}\) および \(C\) で囲まれる図形の面積を求めよ.
考え方
接線の方程式
\(y=f(x)\) 上の接点 \(( t , f(t) )\) における接線の方程式は
\(y-f(t)=f^{\prime}(t)(x-t)\)
解と係数の関係
\(x=\alpha\) ,\(\beta\) を解とする \(2\) 次方程式の \(1\) つは
\(x^2-(\alpha+\beta)x+\alpha\beta=0\)
固まりで積分
数学 Ⅲ を勉強している人にとっては常識的な公式ですが、文系の方はこの公式はぜひ使えるようにしておきましょう!これを使えるかどうかで、計算量が劇的に減ります!
例:\(\displaystyle\int (2x+1)^2 \enspace dx=\displaystyle\frac{1}{2\times3}(2x+1)^{3}+C\)
解答・解説
\(C\) と \(L_{1}\) , \(L_{2}\) との接点の \(x\) 座標をそれぞれ \(\alpha\) , \(\beta\) とおく.( \(\alpha<\beta\) )
 \(y=\displaystyle\frac{x^2}{4}\) より \(y^{\prime}=\displaystyle\frac{x}{2}\) であるから,
\(y=\displaystyle\frac{x^2}{4}\) より \(y^{\prime}=\displaystyle\frac{x}{2}\) であるから,
\(L_{1}\) は,\(y-\displaystyle\frac{\alpha^2}{4}=\displaystyle\frac{\alpha}{2}(x-\alpha)\)
よって,\(y=\displaystyle\frac{\alpha}{2}x-\displaystyle\frac{\alpha^2}{4}\) ・・・①
同様に \(L_{2}\) は,\(y=\displaystyle\frac{\beta}{2}x-\displaystyle\frac{\beta^2}{4}\) ・・・②
\(2\) 直線 \(L_{1}\) , \(L_{2}\) は直交するので,
\(\displaystyle\frac{\alpha}{2}\times \displaystyle\frac{\beta}{2}=-1\)
よって,\(\alpha\beta=-4\) ・・・③
また,①,②の交点の \(x\) 座標は \(\displaystyle\frac{3}{2}\) であるから
\(\displaystyle\frac{\alpha}{2}\times \displaystyle\frac{3}{2}-\displaystyle\frac{\alpha^2}{4}=\displaystyle\frac{\beta}{2}\times \displaystyle\frac{3}{2}-\displaystyle\frac{\beta^2}{4}\)
\(\alpha^2-3\alpha=\beta^2-3\beta\)
\(\alpha^2-\beta^2-3(\alpha-\beta)=0\)
\((\alpha-\beta)(\alpha+\beta-3)=0\)
\(\alpha\not=\beta\) より \(\alpha+\beta=3\) ・・・④
③,④より \(\alpha\) , \(\beta\) は
\(t^2-3t-4=0\) の \(2\) つの実数解である
\((t+1)(t-4)=0\)
\(t = -1 , 4\)
よって,\(\alpha=–1\) , \(\beta=4\)
したがって求める面積は
\(\displaystyle\int^{\frac{3}{2}}_{-1}\left\{\displaystyle\frac{x^2}{4}-\left(-\displaystyle\frac{1}{2}x-\displaystyle\frac{1}{4}\right)\right\}dx+\displaystyle\int^{4}_{\frac{3}{2}}\left\{\displaystyle\frac{x^2}{4}-(-2x-4)\right\}dx\)
\(=\displaystyle\frac{1}{4}\displaystyle\int^{\frac{3}{2}}_{-1}(x+1)^2 dx+\displaystyle\frac{1}{4}\displaystyle\int^{4}_{\frac{3}{2}}(x-4)^2 dx\)
\(=\displaystyle\frac{1}{4}\Bigl[\displaystyle\frac{1}{3}(x+1)^3\Bigr]^{\frac{3}{2}}_{-1}+\displaystyle\frac{1}{4}\Bigl[\displaystyle\frac{1}{3}(x-4)^3\Bigr]^{4}_{\frac{3}{2}}\)
\(=\displaystyle\frac{125}{48}\)
参考:共通テスト裏技公式!
覚えておいてほしい裏技公式
《注意》以下は記述の解答では使用できません!
下図のような放物線の2接線の交点の \(x\) 座標について
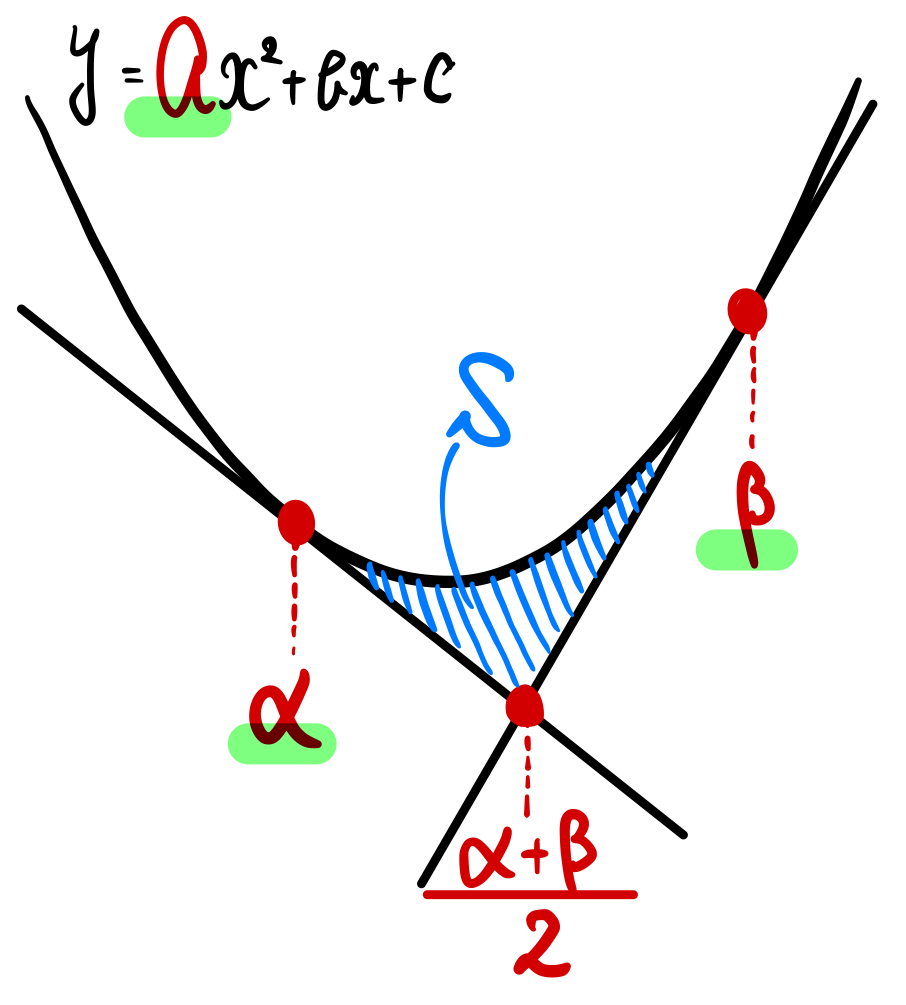
・2 接点を \(x=\alpha\),\(\beta\) のとき、2 接線の交点の \(x\) 座標は各接点の”中点”になる
・放物線と 2 接線で囲まれた面積は、\(S=\displaystyle\frac{a}{12}(\beta-\alpha)^3\)
(※ \(a\) は放物線の 2 乗の係数)
・面積 \(S\) は \(x=\displaystyle\frac{\alpha+\beta}{2}\) で 2 等分される









コメント