【2021名古屋大学・文(第1問)】
\(a\) を正の実数とする.放物線 \(y=x^2\) を \(C_{1}\) 、放物線 \(y=-x^2+4ax-4a^2+4a^4\) を \(C_{2}\) とする.以下の問に答えよ.
(1) 点 \(( t , t^2 )\) における \(C_{1}\) の接線の方程式を求めよ.
(2) \(C_{1}\) と \(C_{2}\) が異なる 2 つの共通接線 \(L\)、\(L’\) を持つような \(a\) の範囲を求めよ.ただし、\(C_{1}\) と \(C_{2}\) の共通接線とは、\(C_{1}\) と \(C_{2}\) の両方に接する直線のことである.
(3) \(L\)、\(L’\) の交点の座標を求めよ.
(4) \(C_{1}\) と \(L\)、\(L’\) で囲まれた領域を \(D_{1}\) とし、不等式 \(x≦a\) の表す領域を \(D_{2}\) とする.\(D_{1}\) と \(D_{1}\) の共通部分の面積 \(S(a)\) を求めよ.
考え方・Pointまとめ
(1)接線の方程式
\(y=f(x)\) 上の接点 \(( t , f(t) )\) における接線の方程式は
\(y-f(t)=f^{\prime}(t)(x-t)\)
(2)共通接線
共通接線については、【数学Ⅱ・微分】共通接線2タイプの解法まとめ に考え方・解法パターンをまとめています。

(3)解と係数の関係
\(ax^2+bx+c=0\) の \(2\) つの解を \(\alpha\) ,\(\beta\) とすると
\(\alpha+\beta=-\displaystyle\frac{b}{a}\) ,\(\alpha \beta=\displaystyle\frac{c}{a}\)
(4)固まりで積分
数学 Ⅲ を勉強している人にとっては常識的な公式ですが、文系の方はこの公式はぜひ使えるようにしておきましょう!これを使えるかどうかで、計算量が劇的に減ります!
例:\(\displaystyle\int (2x+1)^2 \enspace dx=\displaystyle\frac{1}{2\times3}(2x+1)^{3}+C\)
解答
(1)
\(f(x)=x^2\)、\(g(x)=-x^2+4ax-4a^2+4a^4\) とおく.
\(f^{\prime}(x)=2x\) より
\(( t , t^2 )\) における接線の方程式は
\(y-t^2=2t(x-t)\)
\(y=2tx-t^2\) ・・・ ①
(2)
①と \(y=g(x)\) が接するとき、
\(2tx-t^2=-x^2+4ax-4a^2+4a^4\)
\(x^2+2(t-2a)x-t^2+4a^2-4a^4=0\)
②の(判別式) = 0 となればよいので、
\((t-2a)^2-(-t^2+4a^2-4a^4)=0\)
\(t^2-2at+2a^4=0\) ・・・ ②
また、共通接線を 2 本持つためには、②が異なる 2 実解を持てばよいので、
②の(判別式) > 0 を満たせばよい.
\(a^2-4a^4>0\)
\(a^2>0\) より \(2a^2-1<0\)
\(a>0\) から
\(0<a<\displaystyle\frac{1}{\sqrt{2}}\) ・・・ ③
(3)
③のとき、②の 2 解を \(\alpha , \beta\) とおく.\(( \alpha < \beta )\)
解と係数の関係より
\(\begin{cases}\alpha+\beta=2a\\ \alpha \beta=2a^4\end{cases}\) ・・・ ④
①より、2 接線は
\(y=2\alpha x-\alpha^2\)
\(y=2\beta x-\beta^2\)
これらの交点は \(( x , y )=\displaystyle\left( \displaystyle\frac{\alpha+\beta}{2} , \alpha \beta \right)\)
④より、\(P ( a , 2a^4 )\)
(4)
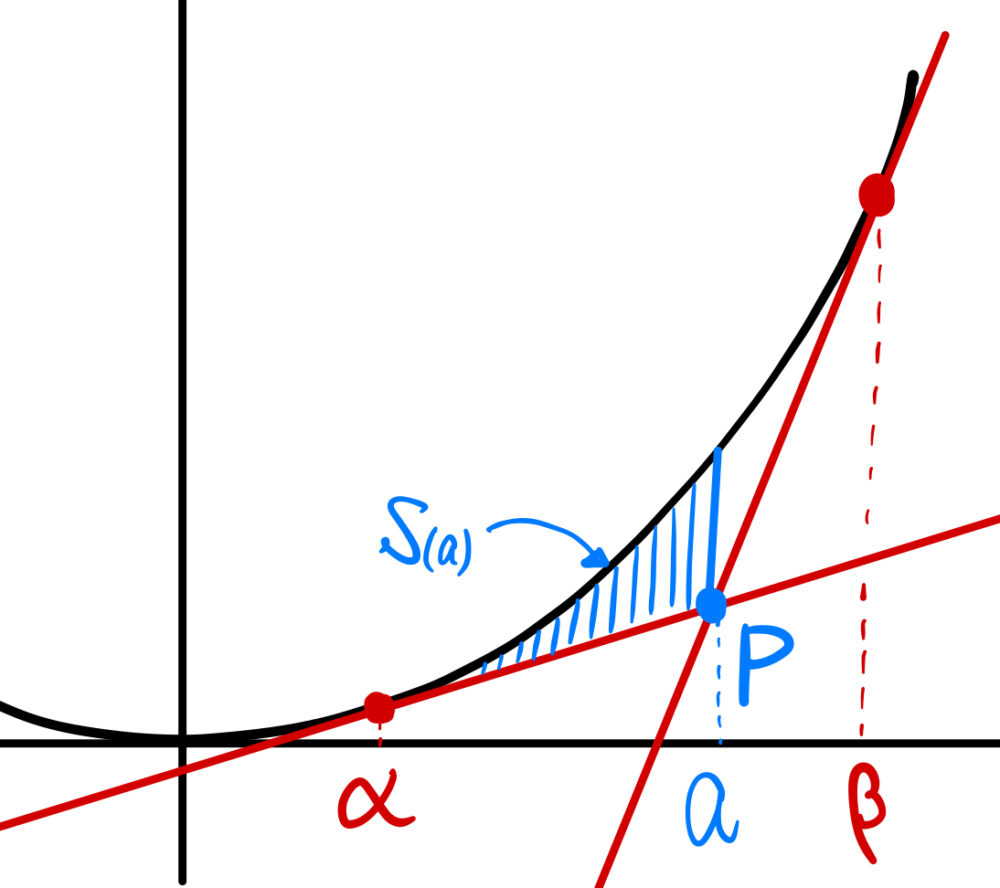
\(S(a)= \displaystyle\int_{\alpha}^{a}\left\{(x^2-(2\alpha x-\alpha^2) \right\}\enspace dx \)
\(S(a)= \displaystyle\int_{\alpha}^{\frac{\alpha+\beta}{2}}(x-\alpha)^2\enspace dx \)
\(=\left[\displaystyle\frac{1}{3}(x-\alpha)^3\right] _{\alpha}^{\frac{\alpha+\beta}{2}}\)
\(=\displaystyle\frac{1}{24}(\beta-\alpha)^3\)
ここで、②を解くと
\(t=a\pm\sqrt{a^2-2a^4}\) より
\(\beta-\alpha=2\sqrt{a^2-2a^4}\)
したがって、
\(S(a)= \displaystyle\frac{1}{3}\left(\sqrt{a^2-2a^4}\right)^3\)
参考:共通テスト裏技公式!
(3) , (4)について覚えておいてほしい裏技公式
《注意》以下は記述の解答では使用できません!
下図のような放物線の2接線の交点の \(x\) 座標について
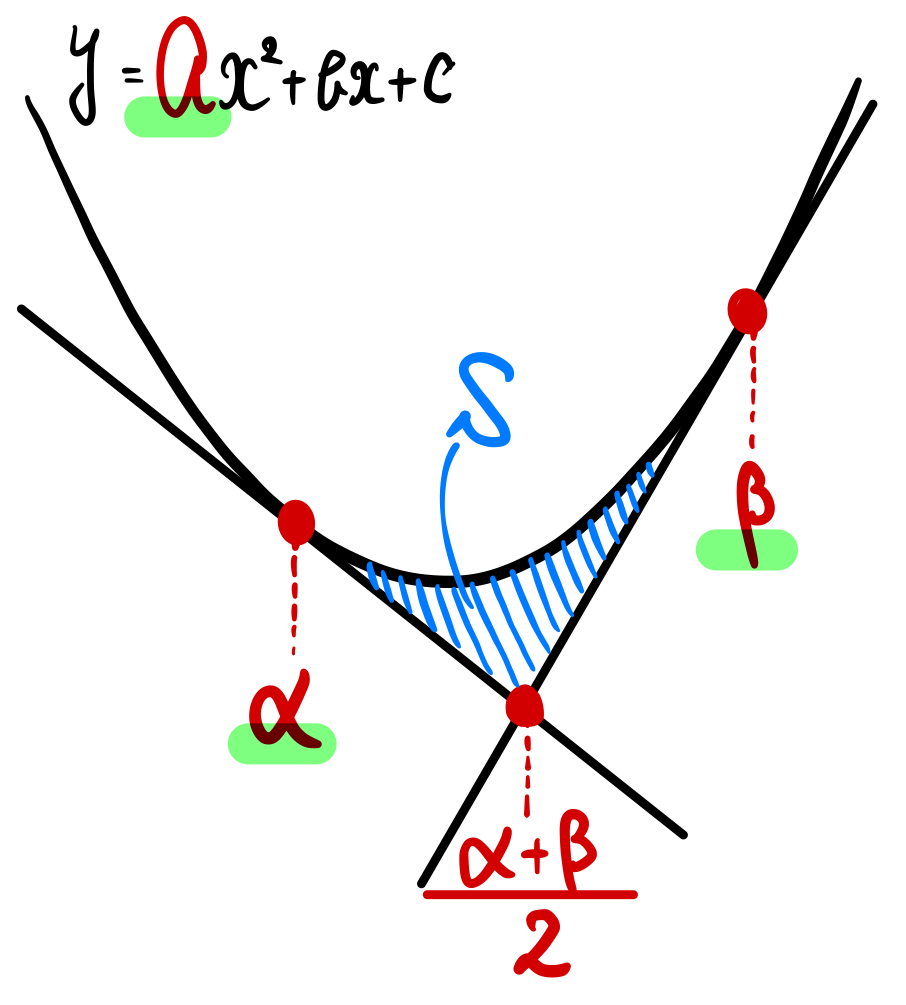
・2 接点を \(x=\alpha\),\(\beta\) のとき、2 接線の交点の \(x\) 座標は各接点の”中点”になる
・放物線と 2 接線で囲まれた面積は、\(S=\displaystyle\frac{a}{12}(\beta-\alpha)^3\)
(※ \(a\) は放物線の 2 乗の係数)
・面積 \(S\) は \(x=\displaystyle\frac{\alpha+\beta}{2}\) で 2 等分される









コメント