【2023数学ⅡB(第1日程)：第５問ベクトル】

(１)(２)問題と解答・解説《ア〜キ》

(１)(２)解答・解説《ア〜キ》

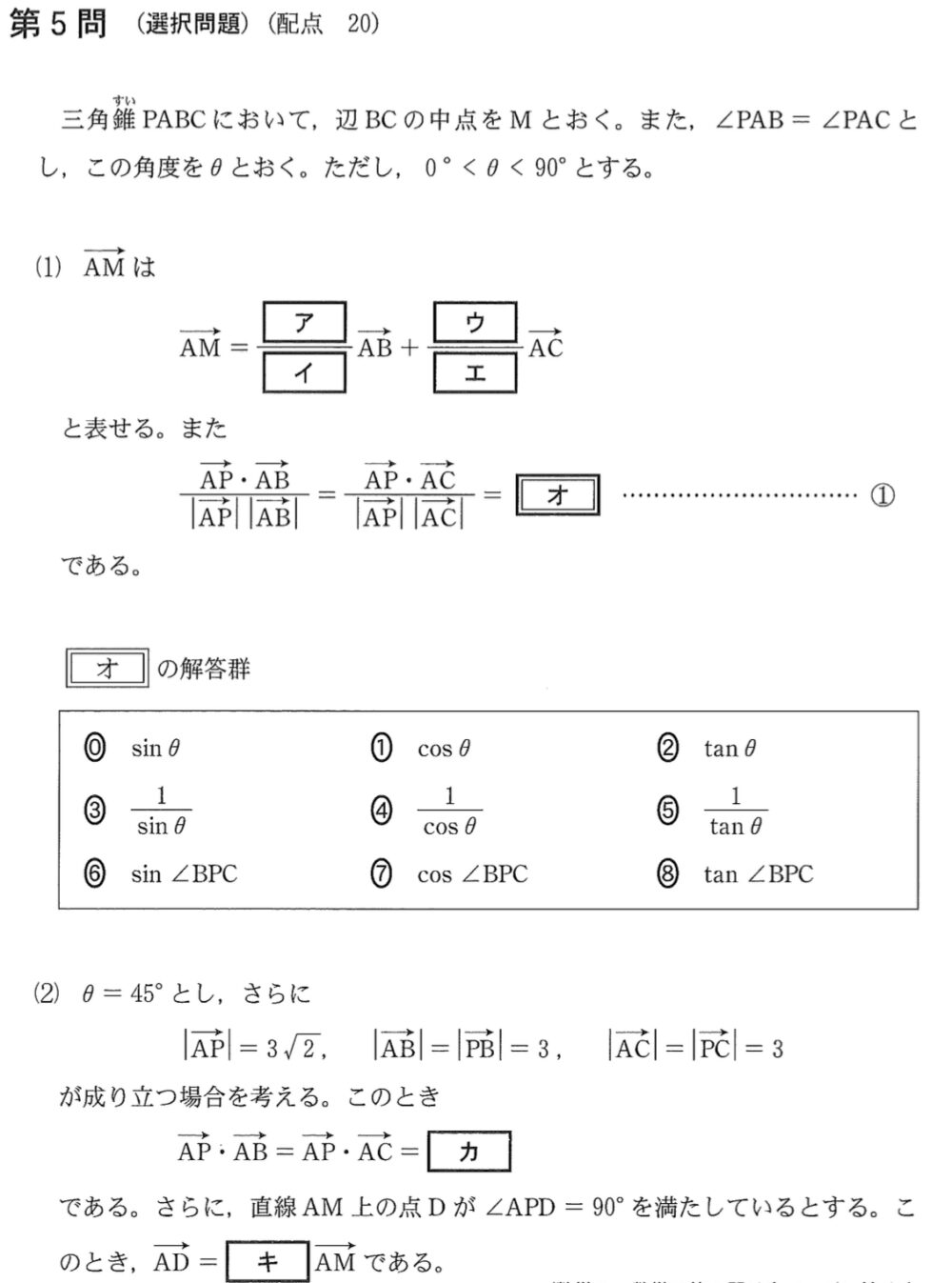
(１)　点 \(M\) は \(BC\) の中点より

\(\overrightarrow{AM}=\displaystyle\frac{1}{2}\overrightarrow{AB}+\displaystyle\frac{1}{2}\overrightarrow{AC}\) ・・・《ア〜エ》

また，\(\angle PAB=\angle PAC\) より

\(\cos\angle PAB=\cos\angle PAC=\cos\theta\)

よって，\(\displaystyle\frac{\overrightarrow{AP}\cdot\overrightarrow{AB}}{\left|\overrightarrow{AP}\right|\left|\overrightarrow{AB}\right|}=\displaystyle\frac{\overrightarrow{AP}\cdot\overrightarrow{AC}}{\left|\overrightarrow{AP}\right|\left|\overrightarrow{AC}\right|}=\)\(\cos \theta\) ・・・《オ：①》

(２)　\(\theta=45°\)，\(\left|\overrightarrow{AP}\right|=3\sqrt{2}\)，\(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{PB}\right|=\left|\overrightarrow{AC}\right|=\left|\overrightarrow{PC}\right|=3\) より

\(\displaystyle\frac{\overrightarrow{AP}\cdot\overrightarrow{AB}}{3\sqrt{2}\times 3}=\displaystyle\frac{\overrightarrow{AP}\cdot\overrightarrow{AC}}{3\sqrt{2}\times 3}=\cos  45°\)

よって，\(\overrightarrow{AP}\cdot\overrightarrow{AB}=\overrightarrow{AP}\cdot\overrightarrow{AC}=9\) ・・・《カ》

点 \(D\) は \(AM\) 上より，実数 \(t\) を用いて

\(\overrightarrow{AD}=t\overrightarrow{AM}=\displaystyle\frac{t}{2}\overrightarrow{AB}+\displaystyle\frac{t}{2}\overrightarrow{AC}\) とおける．

\(\angle APD=90°\) より \(\overrightarrow{AP}\cdot\overrightarrow{PD}=0\)

\(\overrightarrow{AP}\cdot\left(\overrightarrow{AD}-\overrightarrow{AP}\right)=0\)

\(\overrightarrow{AP}\cdot\overrightarrow{AD}-\left|\overrightarrow{AP}\right|^2=0\)

\(\overrightarrow{AP}\cdot\left(\displaystyle\frac{t}{2}\overrightarrow{AB}+\displaystyle\frac{t}{2}\overrightarrow{AC}\right)-\left|\overrightarrow{AP}\right|^2=0\)

\(\displaystyle\frac{t}{2}\overrightarrow{AP}\cdot\overrightarrow{AB}+\displaystyle\frac{t}{2}\overrightarrow{AP}\cdot\overrightarrow{AC}-\left|\overrightarrow{AP}\right|^2=0\)

\(\displaystyle\frac{9t}{2}+\displaystyle\frac{9t}{2}-18=0\)

\(t=2\)

よって，\(\overrightarrow{AD}=2\overrightarrow{AM}\) ・・・《キ》

(３)( ⅰ )問題と解答・解説《クケ》

(３)( ⅰ )解答・解説《クケ》

\(\overrightarrow{AQ}=2\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}\) のとき

\(\overrightarrow{PQ}=\overrightarrow{AQ}-\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AP}\) であり

\(\overrightarrow{AP}\cdot\overrightarrow{PQ}=0\) より

\(\overrightarrow{AP}\cdot\left(\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AP}\right)=0\)

\(\overrightarrow{AP}\cdot\overrightarrow{AB}+\overrightarrow{AP}\cdot\overrightarrow{AC}=\overrightarrow{AP}\cdot\overrightarrow{AP}\) ・・・《ク：⓪》

\(\displaystyle\frac{\overrightarrow{AP}\cdot\overrightarrow{AB}}{\left|\overrightarrow{AP}\right|\left|\overrightarrow{AB}\right|}=\displaystyle\frac{\overrightarrow{AP}\cdot\overrightarrow{AC}}{\left|\overrightarrow{AP}\right|\left|\overrightarrow{AC}\right|}=\cos \theta\) より

\(\overrightarrow{AP}\cdot\overrightarrow{AB}=\left|\overrightarrow{AP}\right|\left|\overrightarrow{AB}\right|\cos \theta\)，\(\overrightarrow{AP}\cdot\overrightarrow{AC}=\left|\overrightarrow{AP}\right|\left|\overrightarrow{AC}\right|\cos \theta\) なので

\(\left|\overrightarrow{AP}\right|\left|\overrightarrow{AB}\right|\cos \theta+\left|\overrightarrow{AP}\right|\left|\overrightarrow{AC}\right|\cos \theta=\left|\overrightarrow{AP}\right|^2\)

\(\left|\overrightarrow{AB}\right|\cos \theta+\left|\overrightarrow{AC}\right|\cos \theta=\left|\overrightarrow{AP}\right|\) ・・・《ケ：③》

(３)( ⅱ )問題と解答・解説《コ〜シ》

(３)( ⅱ )解答・解説《コ〜シ》

\(k\) を正の定数とし

\(k\overrightarrow{AP}\cdot\overrightarrow{AB}=\overrightarrow{AP}\cdot\overrightarrow{AC}\) が成立するとする．

\(\overrightarrow{AP}\cdot\overrightarrow{AB}=\left|\overrightarrow{AP}\right|\left|\overrightarrow{AB}\right|\cos \theta\)，\(\overrightarrow{AP}\cdot\overrightarrow{AC}=\left|\overrightarrow{AP}\right|\left|\overrightarrow{AC}\right|\cos \theta\) より

\(k\left|\overrightarrow{AP}\right| \left|\overrightarrow{AB}\right|\cos \theta=\left|\overrightarrow{AP}\right| \left|\overrightarrow{AC}\right|\cos \theta\)

\(k\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AC}\right|\) ・・・《コ：⓪》

\(\left|\overrightarrow{AB}\right|\cos \theta+\left|\overrightarrow{AC}\right|\cos \theta=\left|\overrightarrow{AP}\right|\) ・・・②

\(k\left|\overrightarrow{AB}\right|=\left|\overrightarrow{AC}\right|\) ・・・③　とおく．

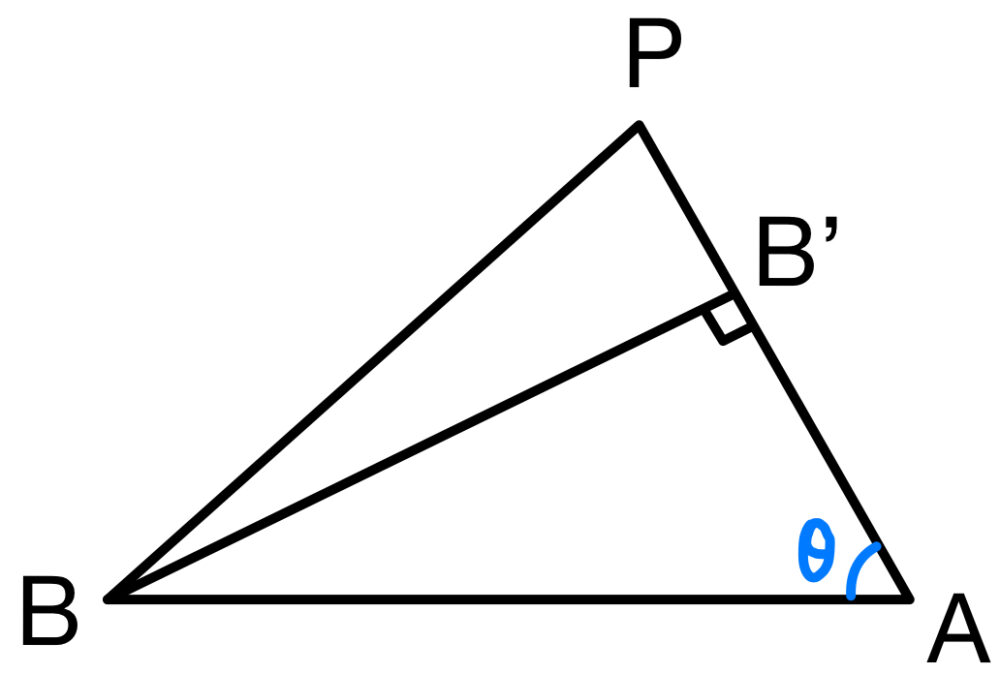
右図より \(\triangle ABB^{\prime}\) に注目すると

\(\cos \theta=\displaystyle\frac{\left|\overrightarrow{AB^{\prime}}\right|}{\left|\overrightarrow{AB}\right|}\) より

\(\left|\overrightarrow{AB^{\prime}}\right|=\left|\overrightarrow{AB}\right|\cos \theta\)

同様に \(\triangle ACC^{\prime}\) に注目して考えると \(\left|\overrightarrow{AC^{\prime}}\right|=\left|\overrightarrow{AC}\right|\cos \theta\)

②より \(\left|\overrightarrow{AB^{\prime}}\right|+\left|\overrightarrow{AC^{\prime}}\right|=\left|\overrightarrow{AP}\right|\) ・・・④

③より \(\left|\overrightarrow{AB^{\prime}}\right|：\left|\overrightarrow{AC^{\prime}}\right|=\left|\overrightarrow{AB}\right|：\left|\overrightarrow{AC}\right|=1：k\) ・・・⑤

④，⑤より

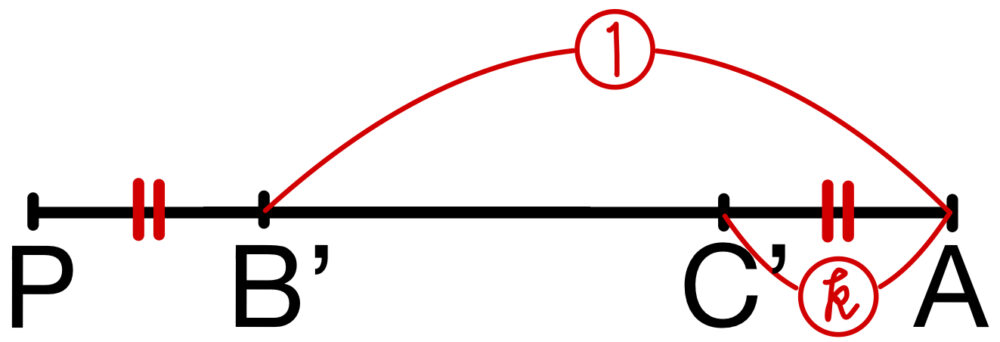
\(\left|\overrightarrow{AC^{\prime}}\right|=\left|\overrightarrow{B^{\prime}P}\right|\) となり

《サ：④ \(B^{\prime}\) と \(C^{\prime}\) が線分 \(AP\) をそれぞれ \(1：k\) と \(k：1\) に内分する点》

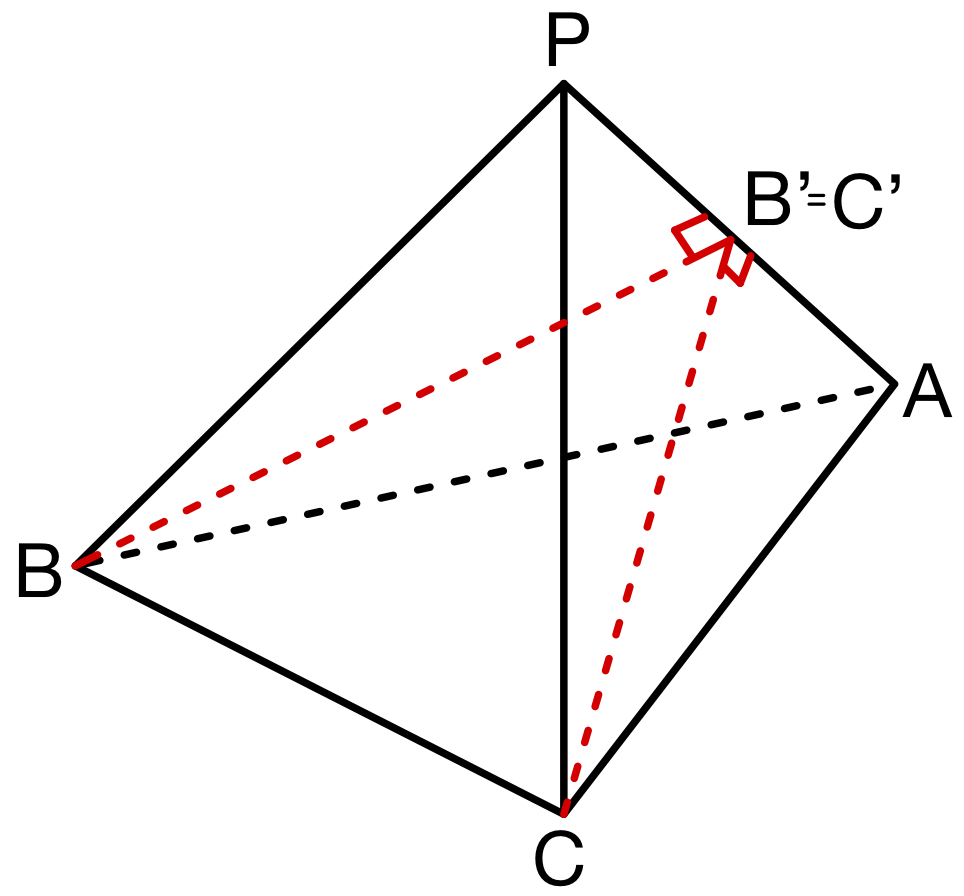特に \(k=1\) のとき

つまり \(B^{\prime}\) と \(C^{\prime}\) が一致 ( \(AP\) の中点となる ) とき

点 \(B\)，\(C\) からそれぞれ \(AP\) に下ろした垂線の足が中点となるので，

《シ：\(\triangle PAB\) と \(\triangle PAC\) がそれぞれ \(BP=BA\)，\(CP=CA\) を満たす二等辺三角形 》となる．