【2021数学ⅡB(第１日程)】第１問[２](指数・対数関数)

(１)問題と解答・解説《セ〜テ》

解答・解説《セ〜テ》

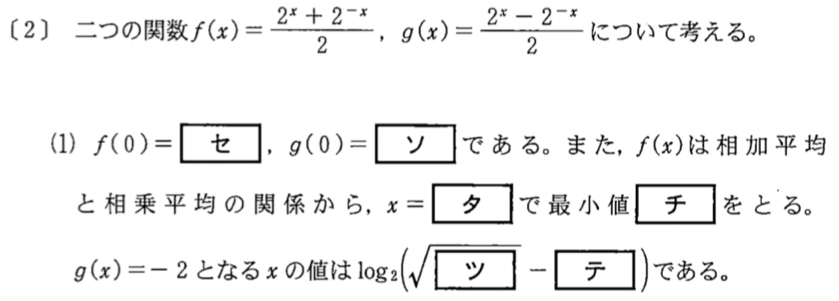
\(f(0)=\displaystyle\frac{2^0+2^{-0}}{2}=\)\(1\) ・・・《セ》

\(g(0)=\displaystyle\frac{2^0-2^{-0}}{2}=\)\(0\) ・・・《ソ》

また，\(2^x>0\) より，相加平均・相乗平均の関係から

\(2^x+2^{-x}≧2\sqrt{2^x\cdot2^{-x}}=2\)

よって，\(f(x)=\displaystyle\frac{2^x+2^{-x}}{2}≧1\)

等号成立は，\(2^x=2^{-x}\) \(\iff\) \(x=0\)

したがって，\(x=0\) で最小値： \(1\) ・・・《タチ》

次に，\(g(x)=-2\) のとき

\(g(x)=\displaystyle\frac{2^x-2^{-x}}{2}=-2\)

\(a=2^x\) とおく ( \(a>0\) )

\(\displaystyle\frac{a-\displaystyle\frac{1}{a}}{2}=-2\)

\(\iff\) \(a^2+4a-1=0\)

\(a>0\) より \(a=-2+\sqrt{5}\)

つまり，\(2^x=-2+\sqrt{5}\)

よって，\(x=\log_{2}{(\sqrt{5}-2)}\) ・・・《ツテ》

(２)問題と解答・解説《ト〜ヌ》

解答・解説《ト〜ヌ》

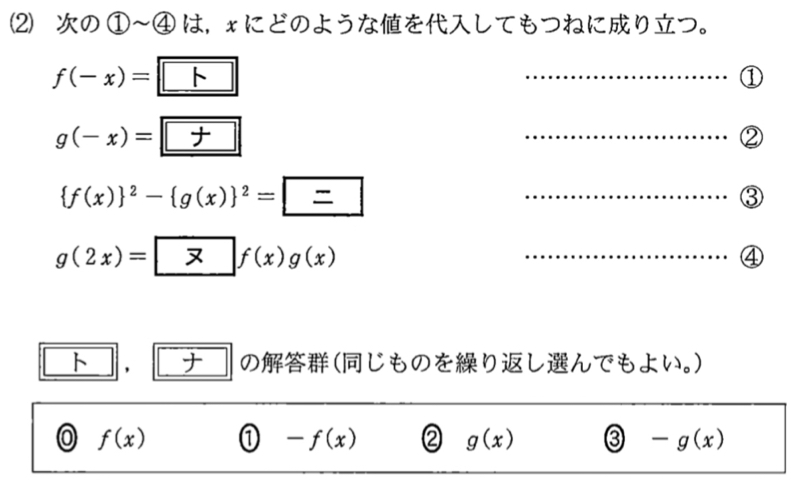
\(f(-x)=\displaystyle\frac{2^{-x}+2^{-(-x)}}{2}=\displaystyle\frac{2^x+2^{-x}}{2}=f(x)\)

よって，\(f(-x)=f(x)\) ・・・《ト：⓪》

\(g(-x)=\displaystyle\frac{2^{-x}-2^{-(-x)}}{2}=-\displaystyle\frac{2^x-2^{-x}}{2}=-g(x)\)

よって，\(g(-x)=-g(x)\) ・・・《ナ：③》

また，

\(\left\{f(x)\right\}^2-\left\{g(x)\right\}^2=\left(f(x)+g(x)\right)\left(f(x)-g(x)\right)=2^x\cdot2^{-x}=\)\(1\) ・・・《ニ》

\(g(2x)=\displaystyle\frac{2^{2x}-2^{-2x}}{2}=\displaystyle\frac{(2^x)^2-(2^{-x})^2}{2}=\displaystyle\frac{(2^x+2^{-x})(2^x-2^{-x})}{2}\) であるから，

\(g(2x)=2\times \displaystyle\frac{2^x+2^{-x}}{2}\times \displaystyle\frac{2^x-2^{-x}}{2}=\)\(2f(x)g(x)\)  ・・・《ヌ》

(３)問題と解答・解説《ネ》

解答・解説《ネ》

(１)より \(f(0)=1\) , \(g(0)=0\) であるから，(A)〜(D) において \(\beta=0\) とする

(A) について

\(f(\alpha)=f(\alpha)g(0)+g(\alpha)f(0)=g(\alpha)\) となるが，

常に \(f(x)=g(x)\) とはならないため，(A) は不成立．

(B) について

\(f(\alpha)=f(\alpha)f(0)+g(\alpha)g(0)=f(\alpha)\) であるから (B) は答えの可能性あり！

(C) について

\(g(\alpha)=f(\alpha)f(0)+g(\alpha)g(0)=f(\alpha)\) となるが，

常に \(f(x)=g(x)\) とはならないため，(A) は不成立．

(D) について

\(g(\alpha)=f(\alpha)g(0)-g(\alpha)f(0)=-g(\alpha)\) となるが，

常に \(g(x)=-g(x)\) とはならないため，(A) は不成立．

以上から，(B) 以外の三つは成り立たない ・・・《ネ：①》

【2021共通テスト(第１日程)】数学ⅡB：第２問(微分法・積分法)｜放物線,3次関数の共有点における接線

放物線の共有点における接線。それと囲まれた図形の面積(3分の1公式)。また３次関数の共有点における接線の方程式。グラフの概形の選択。大学共通テスト対策。センター試験過去問演習。数学ⅡB：微分法・積分法

mathmathmanabu.com

2022.09.17

【2021共通テスト(第1日程)】数学ⅡB：第１問[１](三角関数)｜sin,cosの合成・最大値

サインとコサインの合成をすることで、yの値域(最大値)を求める問題。典型・頻出問題。大学共通テスト対策。センター試験過去問演習。数学ⅡB：三角関数

mathmathmanabu.com

2022.09.15