(1)問題《ア~キ》
(1)解答・解説《ア~キ》
(ⅰ) \(y=log_{3}{x} \) のグラフは
\(x=27\) のとき \( y=log_{3}{27}=log_{3}{3^3}=3\) より \((27,3)\) ・・・《ア》を通る.
また,\(y=log_{2}{\displaystyle\frac{x}{5}}\) のグラフは
\(y=1\) のとき \(1=log_{2}{\displaystyle\frac{x}{5}}\) \(\iff\) \(\displaystyle\frac{x}{5}=2\)
よって \(x=10\) なので,\((10,1)\) ・・・《イウ》を通る.
(ⅱ) \(y=\log_{k}{x}\) のグラフは,\(k\) の値によらず定点 \((1,0)\) ・・・《エオ》を通る.
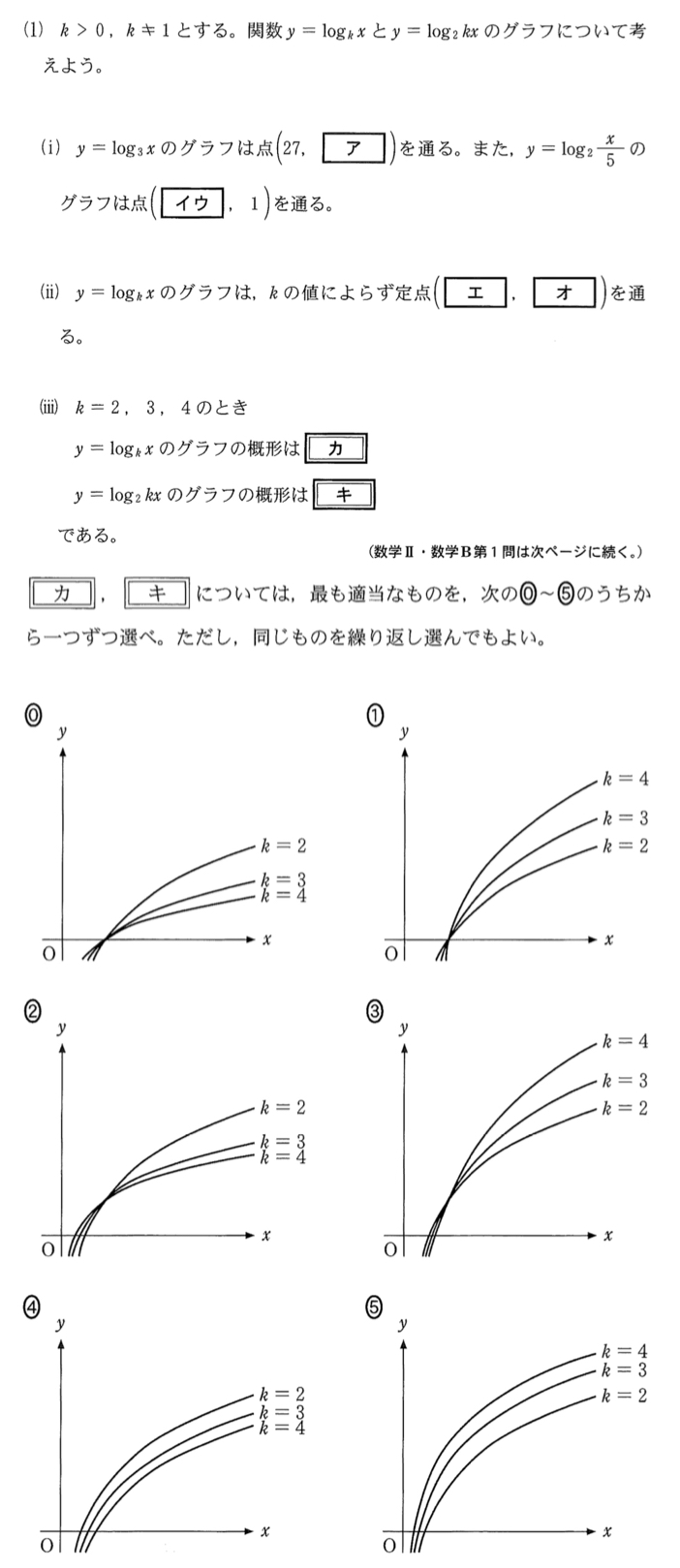
(ⅲ) \(k=2,3,4\) のとき \(y=log_{k}{x}\) のグラフ
(ⅱ)より,\(y=\log_{k}{x}\) のグラフは,\(k\) の値によらず定点 \((1,0)\) を通るので,答えの可能性は『 ⓪ or ① 』
ここで,\(x=4\) として考えてみる.
\(k=2\) のとき \(y=\log_{2}{4}=2\)
\(k=4\) のとき \(y=\log_{4}{4}=1\) であるから,これを満たすのは ⓪ ・・・《カ》
また \(y=\log_{2}{kx}\) のグラフについて
\(y=\log_{2}{kx}=\log_{2}{x}+\log_{2}{k}\)
これは \(y=\log_{2}{x}\) のグラフを \(y\) 軸方向に \(\log_{2}{k}\) だけ平行移動したグラフであるから,⑤ ・・・《キ》
(2)(ⅰ)問題《ク》
(2)(ⅰ)解答・解説《ク》
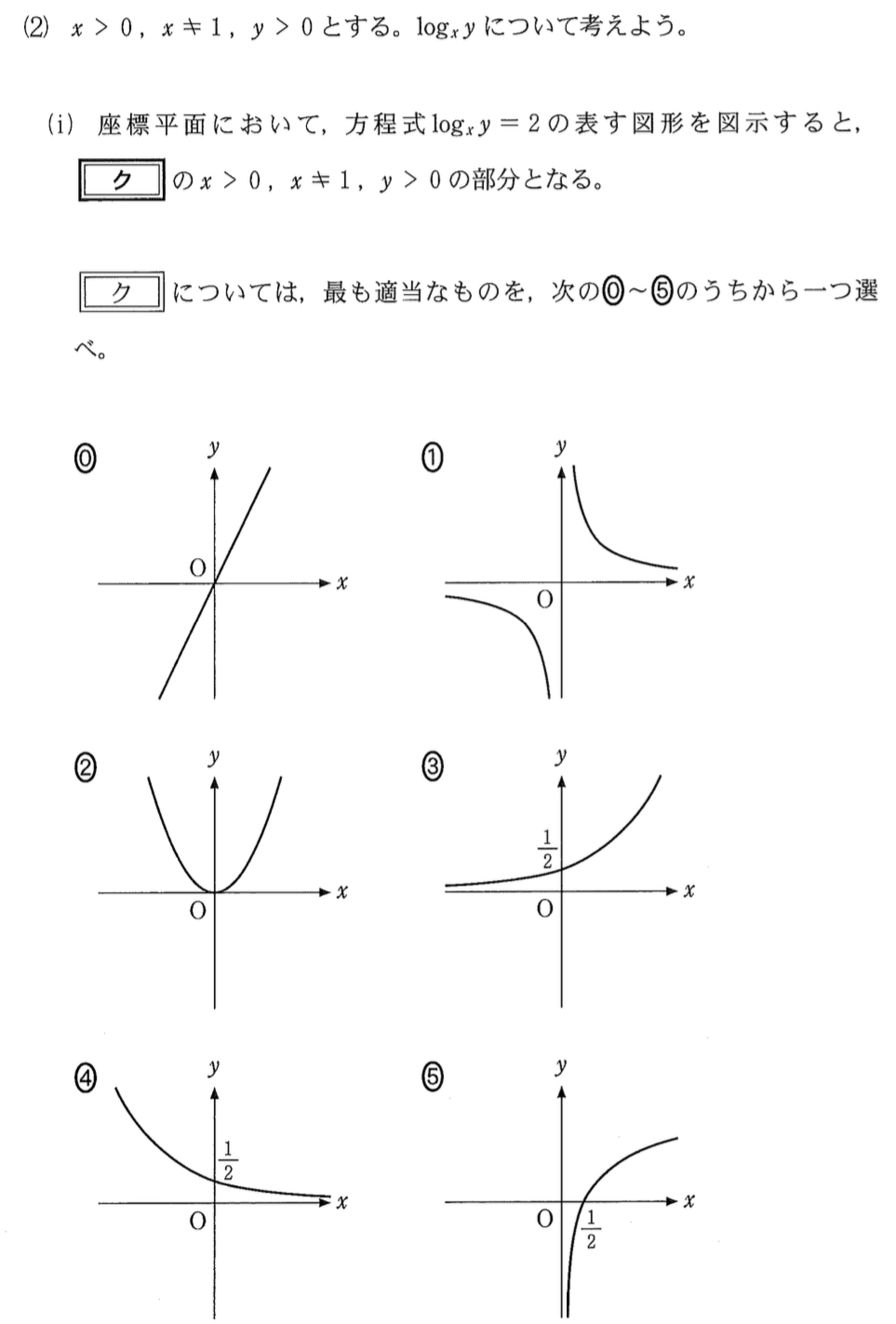
\(log_{x}{y}=2\) \(\iff\) \(y=x^2\) より
放物線 \(y=x^2\) ・・・《ク:②》の \(x>0\),\(x\not=0\),\(y>0\) の部分となる
(2)(ⅱ)問題《ク》
(2)(ⅱ)解答・解説《ク》
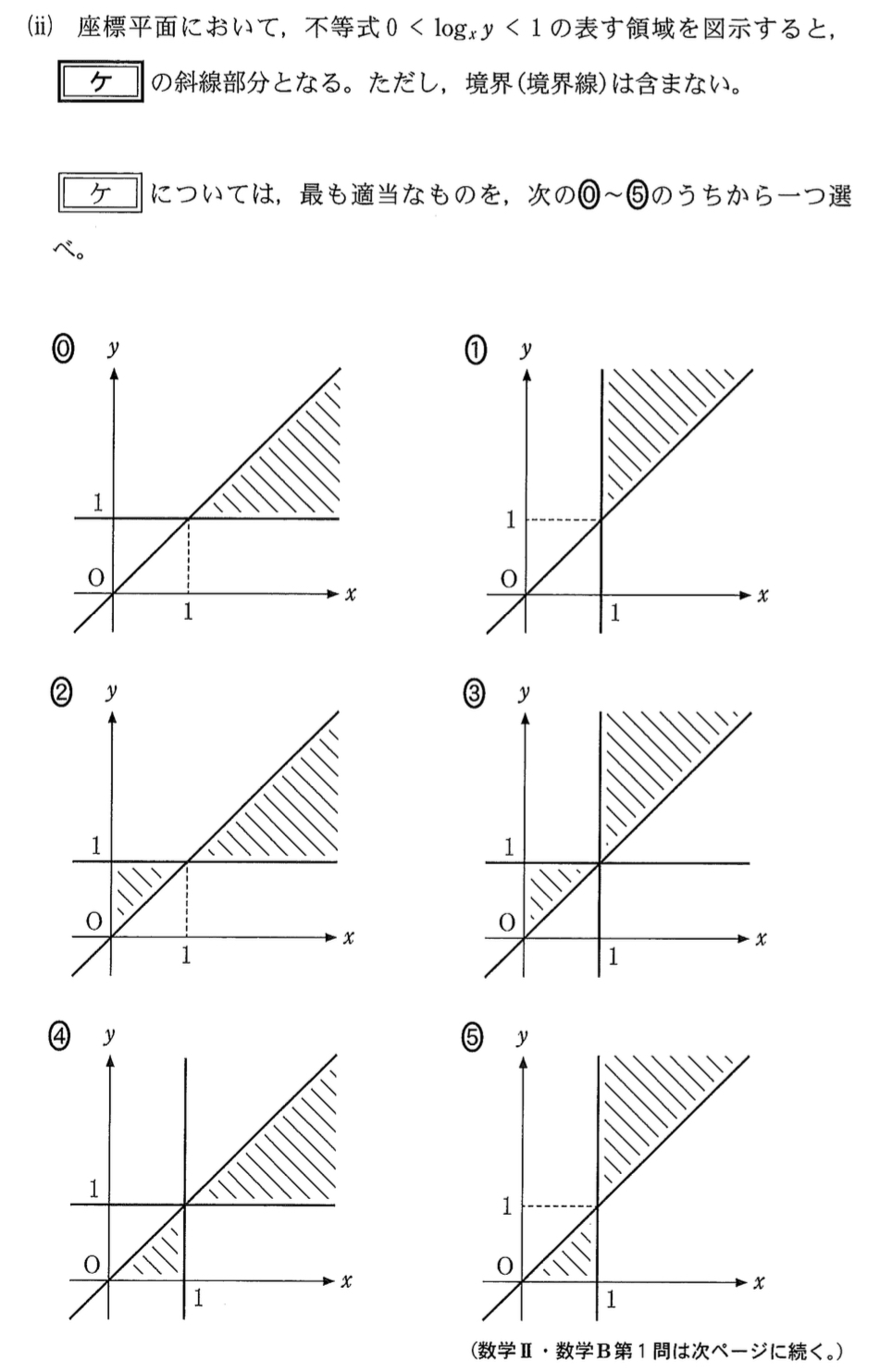
\(0<log_{x}{y}<1\) \(\iff\) \(\log_{x}{1}<\log_{x}{y}<\log_{x}{x}\)
・\(0<x<1\) のとき \(x<y<1\)
・\(x>1\) のとき \(1<y<x\)
これを満たす領域は,②・・・《ケ》








コメント