【2019数学ⅡB：第４問ベクトル】

(１),(２)問題と解答・解説
1. (１),(２)解答・解説《ア〜テ》
(３)問題と解答・解説
1. (３)解答・解説《ト〜ヒ》
(４)問題と解答・解説
1. (４)解答・解説《フ〜ホ》

(１),(２)問題と解答・解説

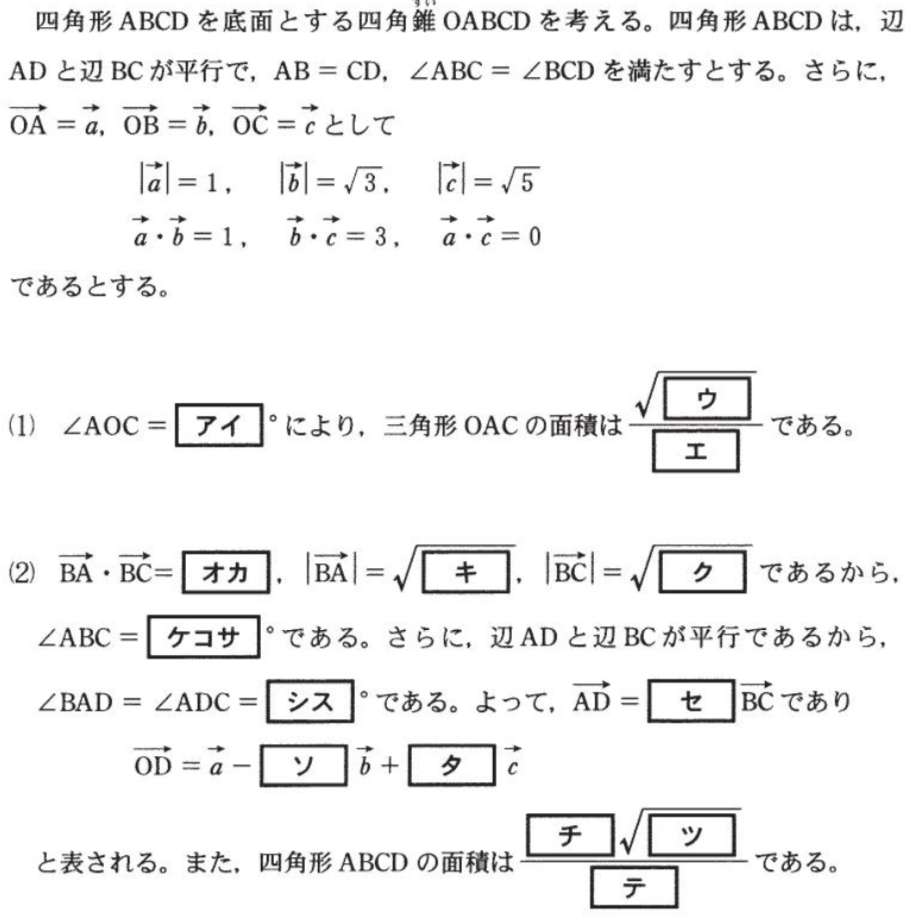
(１),(２)解答・解説《ア〜テ》

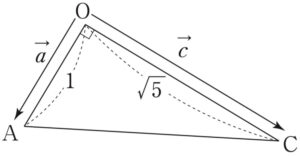(１) \(\overrightarrow{a}\cdot\overrightarrow{c}=0\) より \(\overrightarrow{a}\perp\overrightarrow{c}\) であるから

\(\angle=90°\) ・・・《アイ》

よって \(\triangle OAC=\displaystyle\frac{1}{2}\cdot OA\cdot OC=\) \(\displaystyle\frac{\sqrt{5}}{2}\) ・・・《ウエ》

(２) \(\overrightarrow{BA}\cdot\overrightarrow{BC}=\left(\overrightarrow{a}-\overrightarrow{b}\right)\left(\overrightarrow{c}-\overrightarrow{b}\right)\)

\(=\overrightarrow{a}\cdot\overrightarrow{c}-\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{b}\cdot\overrightarrow{c}+\left|\overrightarrow{b}\right|^2\)

\(=0-1-3+\left(\sqrt{3}\right)^2=\) \(-1\) ・・・《オカ》

\(\left|\overrightarrow{BA}\right|^2=\left|\overrightarrow{a}-\overrightarrow{b}\right|^2\)

\(=\left|\overrightarrow{a}\right|^2-2\overrightarrow{a}\cdot\overrightarrow{b}+\left|\overrightarrow{b}\right|^2\)

\(=1-2\times 1+\left(\sqrt{3}\right)^2=2\)

よって，\(\left|\overrightarrow{BA}\right|=\sqrt{2}\) ・・・《キ》

同様に考え，\(\left|\overrightarrow{BC}\right|=\sqrt{2}\) ・・・《ク》

であるから，

\(\cos \angle ABC=\displaystyle\frac{\overrightarrow{BA}\cdot\overrightarrow{BC}}{\left|\overrightarrow{BA}\right|\left|\overrightarrow{BC}\right|}=\displaystyle\frac{-1}{\sqrt{2}\sqrt{2}}=\displaystyle\frac{-1}{2}\)

よって，\(\angle ABC=120°\) ・・・《ケコサ》

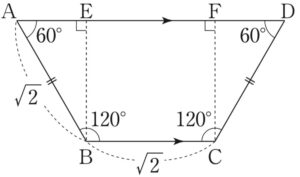
\(AD\) / / \(BC\) かつ \(AB=CD\) より

四角形 \(ABCD\) は等脚台形であるから，

\(\angle BAD=\angle ADC=60°\) ・・・《シス》

右図のように点 \(E\) , \(F\) をとる．

\(AE=\displaystyle\frac{AB}{2}=\displaystyle\frac{\sqrt{2}}{2}\) , \(DF=\displaystyle\frac{CD}{2}=\displaystyle\frac{\sqrt{2}}{2}\) , \(BC=EF=\sqrt{2}\) より \(AD=2\sqrt{2}\)

よって，\(\overrightarrow{AD}=2\overrightarrow{BC}\) ・・・《セ》

であるから，

\(\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{AD}=\overrightarrow{OA}+2\overrightarrow{BC}\)

\(=\overrightarrow{a}+2\left(\overrightarrow{c}-\overrightarrow{b}\right)\) より

\(\overrightarrow{OD}=\overrightarrow{a}-2\overrightarrow{b}+2\overrightarrow{c}\) ・・・《ソタ》

また，\(BE=\displaystyle\frac{\sqrt{3}}{2}AB=\displaystyle\frac{\sqrt{6}}{2}\) より

四角形 \(ABCD\) の面積は，

\(\displaystyle\frac{1}{2}(AD+BC)\cdot BE=\displaystyle\frac{1}{2}(2\sqrt{2}+\sqrt{2})\times \displaystyle\frac{\sqrt{6}}{2}=\) \(\displaystyle\frac{3\sqrt{3}}{2}\) ・・・《チツテ》

(３)問題と解答・解説

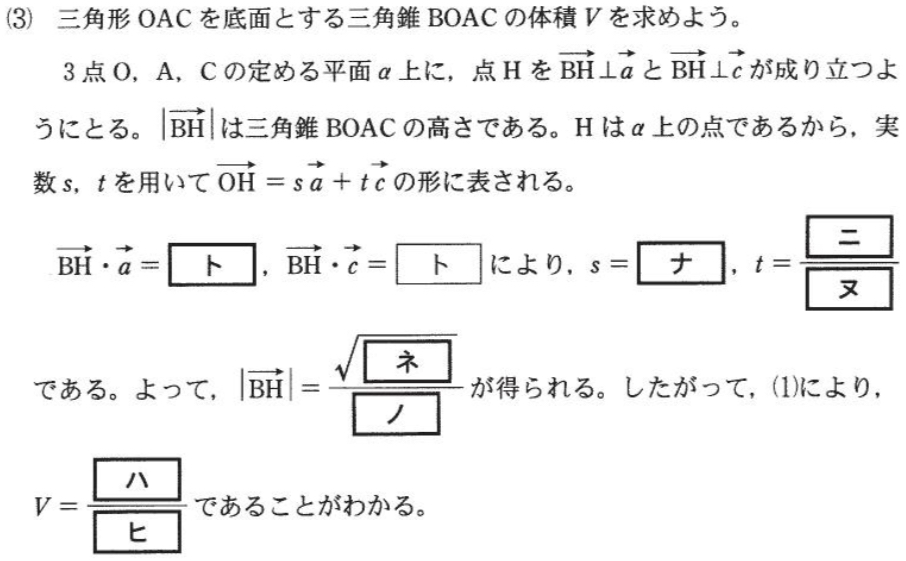
(３)解答・解説《ト〜ヒ》

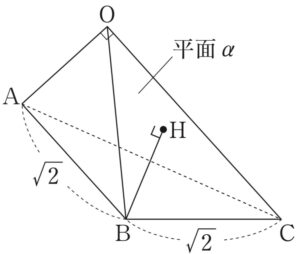
\(\overrightarrow{OH}=s\overrightarrow{a}+t\overrightarrow{c}\) とおく．

\(\overrightarrow{BH}=\overrightarrow{OH}-\overrightarrow{OB}=s\overrightarrow{a}-\overrightarrow{b}+t\overrightarrow{c}\) となり，

\(\overrightarrow{BH}\perp\overrightarrow{a}\) ，\(\overrightarrow{BH}\perp\overrightarrow{c}\) であるから，

\(\overrightarrow{BH}\cdot\overrightarrow{a}=0\) ，\(\overrightarrow{BH}\cdot\overrightarrow{c}=0\) ・・・《ト》

\(\overrightarrow{BH}\cdot\overrightarrow{a}=0\) のとき

\(\left(s\overrightarrow{a}-\overrightarrow{b}+t\overrightarrow{c}\right)\cdot\overrightarrow{a}=0\)

\(s\left|\overrightarrow{a}\right|^2-\overrightarrow{a}\cdot\overrightarrow{b}+t\overrightarrow{a}\cdot\overrightarrow{c}=0\)

\(s-1=0\) \(\iff\) \(s=1\) ・・・《ナ》

\(\overrightarrow{BH}\cdot\overrightarrow{c}=0\) のとき

\(\left(s\overrightarrow{a}-\overrightarrow{b}+t\overrightarrow{c}\right)\cdot\overrightarrow{c}=0\)

\(s\overrightarrow{a}\cdot\overrightarrow{c}-\overrightarrow{b}\cdot\overrightarrow{c}+t\left|\overrightarrow{c}\right|^2=0\)

\(-3+5t=0\) \(\iff\) \(t=\displaystyle\frac{3}{5}\) ・・・《二ヌ》

よって，\(\overrightarrow{BH}=\overrightarrow{a}-\overrightarrow{b}+\displaystyle\frac{3}{5}\overrightarrow{c}\) より

\(\left|\overrightarrow{BH}\right|^2=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+\displaystyle\frac{9}{25}\left|\overrightarrow{c}\right|^2-2\overrightarrow{a}\cdot\overrightarrow{b}-\displaystyle\frac{6}{5}\overrightarrow{b}\cdot\overrightarrow{c}+\displaystyle\frac{6}{5}\overrightarrow{a}\cdot\overrightarrow{c}\)

\(=\displaystyle\frac{1}{5}\)

よって，\(\left|\overrightarrow{BH}\right|=\displaystyle\frac{\sqrt{5}}{5}\) ・・・《ネノ》

したがって，

\(V=\displaystyle\frac{1}{3}\cdot \triangle OAC\cdot\left|\overrightarrow{BH}\right|\)

\(=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{\sqrt{5}}{2}\cdot\displaystyle\frac{\sqrt{5}}{5}=\) \(\displaystyle\frac{1}{6}\) ・・・《ハヒ》