【1992京都大学】
\(\theta\) は \(0°<\theta<90°\) の範囲の角とする.
(1) \(\sin 3\theta=\sin 2\theta\) を満たす \(\theta\) を求めよ.
(2) \(m\),\(n\) を \(0\) 以上の整数とする.\(\theta\) についての方程式
\(\sin 3\theta=m\sin 2\theta+n\sin \theta\)
が解をもつときの \((m,n)\) と,そのときの解 \(\theta\) を求めよ.
\(\sin A=\sin B\) について
考え方①単位円で考える
\(\sin A=\sin B\)
\(\iff\) \(A=B+2n\pi\) または \(A+B=\pi+2n\pi\) ( \(n\) は整数 )
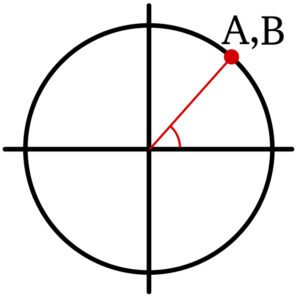 《単位円で \(A\) と \(B\) が同じ位置にあるとき》
《単位円で \(A\) と \(B\) が同じ位置にあるとき》
一番シンプルなのは \(A=B\) ( \(n=0\) のとき )
他にも, \(A\) が \(B\) よりも一周分 ( 2 \(\pi\) 分 ) だけ大きい角度であるとき
\(A=B+2\pi\) ( \(n=1\) のとき )
というように, \(A\) と \(B\) が同じ位置にいるとき, \(A=B+2n\pi\) の関係が成り立つ,
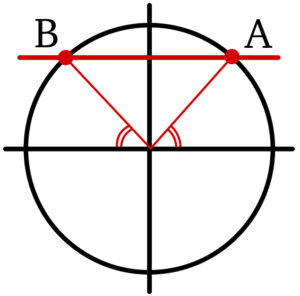 《単位円で \(A\) と \(B\) が同じ高さ(異なる点)のとき》
《単位円で \(A\) と \(B\) が同じ高さ(異なる点)のとき》
例えば,\(\sin 60°=\sin 120°\) のように,
\(60°+120°=180° ( \pi )\) ( \(n=0\) ) のときに成り立つ.
他にも,\(\sin 60°=\sin (60°+360°\times n)\) であるから
\(\sin (60°+360°\times n)=\sin 120°\) となり,
\((60°+360°\times n)+120°=180°+360°\times n ( =\pi+2n\pi)\) の関係が成り立つ.
よって, \(A\) と \(B\) が同じ高さ(異なる点)のとき, \(A+B=\pi+2n\pi\) の関係が成り立つ,

\(\cos A=\cos B\) については,

(1)解答①
\(\sin 3\theta=\sin 2\theta\) より
\(m\) , \(n\) を整数として
\(3\theta=2\theta+2m\pi\) または \(3\theta+2\theta=\pi+2n\pi\) が成り立つ
よって,\(\theta=2m\pi\) または \(\theta=\displaystyle\frac{\pi+2n\pi}{5}\)
\(0<\theta<\displaystyle\frac{\pi}{2}\) を満たすのは,\(n=0\) のとき \(\theta=\displaystyle\frac{\pi}{5}=36°\)
考え方②和積の公式の利用
和積の公式
\(\sin A-\sin B=2\cos\displaystyle\frac{A+B}{2}\sin\displaystyle\frac{A-B}{2}\)
※その他,三角関数に関する公式まとめは「【三角関数】公式まとめ&差がつく入試問題演習」
(1)解答②
\(\sin 3\theta=\sin 2\theta\) \(\iff\) \(\sin 3\theta-\sin 2\theta=0\)
\(\sin 3\theta-\sin 2\theta=2\cos\displaystyle\frac{5\theta}{2}\sin\displaystyle\frac{\theta}{2}=0\)
\(0°<\theta<90°\) より
\(0°<\displaystyle\frac{5\theta}{2}<225°\) , \(0°<\displaystyle\frac{\theta}{2}<45°\) であるから,
\(\displaystyle\frac{5\theta}{2}=90°\)
よって,\(\theta=36°\)
(2) 解答・解説
\(\theta\) は \(0°<\theta<90°\) の範囲の角とする.
(2) \(m\),\(n\) を \(0\) 以上の整数とする.\(\theta\) についての方程式
\(\sin 3\theta=m\sin 2\theta+n\sin \theta\)
が解をもつときの \((m,n)\) と,そのときの解 \(\theta\) を求めよ.
\(3\) 倍角 , \(2\) 倍角の公式より与式は,
\(3\sin \theta-4\sin^3\theta=2m\sin \theta\cos \theta+n\sin \theta\)
\(0°<\theta<90°\) より \(\sin \theta\not=0\) より
\(3-4\sin^2\theta=2m\cos \theta+n\)
\(3-4(1-\cos^2\theta)=2m\cos \theta+n\)
\(4\cos^2 \theta-2m\cos \theta-n-1=0\)
\(t=\cos \theta\) とおく( \(0<t<1\) )
\(4t^2-2mt-n-1=0\)
\(f(t)=4t^2-2mt-n-1\) とおくと
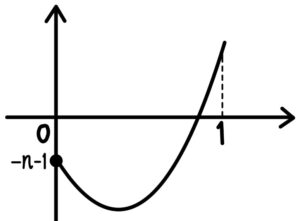 \(f(t)=0\) が \(0<t<1\) で少なくとも \(1\) つ解を持てばよい
\(f(t)=0\) が \(0<t<1\) で少なくとも \(1\) つ解を持てばよい
ここで,\(y=f(t)\) は下に凸の放物線であり,
\(f(0)=-n-1<0\) であることに注目すると
題意を満たすのためには \(f(1)>0\) を満たせばよい.
よって,\(f(1)=-2m-n+3>0\)
\(2m+n<3\)
これを満たす \(0\) 以上の整数 \(m\),\(n\) は
\(( m , n ) = ( 0 , 0 ) , ( 0 , 1 ) , ( 0 , 2 ) , ( 1 , 0 )\)
( ア ) \(( m , n ) = ( 0 , 0 )\) のとき
\(f(t)=4t^2-1=0\)
\(0<t<1\) より \(t=\displaystyle\frac{1}{2}\)
よって,\(\cos \theta=\displaystyle\frac{1}{2}\) より \(\theta=60°\)
( イ ) \(( m , n ) = ( 0 , 1 )\) のとき
\(f(t)=4t^2-2=0\)
\(0<t<1\) より \(t=\displaystyle\frac{\sqrt{2}}{2}\)
よって,\(\cos \theta=\displaystyle\frac{\sqrt{2}}{2}\) より \(\theta=45°\)
( ウ ) \(( m , n ) = ( 0 , 2 )\) のとき
\(f(t)=4t^2-3=0\)
\(0<t<1\) より \(t=\displaystyle\frac{\sqrt{3}}{2}\)
よって,\(\cos \theta=\displaystyle\frac{\sqrt{3}}{2}\) より \(\theta=30°\)
( エ ) \(( m , n ) = ( 1 , 0 )\) のとき
(1) より \(\theta=36°\)
したがって,
\((m,n)=(0,0)\) のとき,\(\theta=60°\)
\((m,n)=(0,1)\) のとき,\(\theta=45°\)
\((m,n)=(0,2)\) のとき,\(\theta=30°\)
\((m,n)=(1,0)\) のとき,\(\theta=36°\)







コメント