【1993京都大学[1]】
\(p>0\) とする.双曲線 \(x^2-y^2=1\) に点 \(P(0,p)\) から \(2\) 本の接線を引いて,それぞれの接点を \(A\),\(B\) とするとき,\(\triangle PAB\) の面積を最小にするような \(p\) の値を求めよ.
双曲線の接線
双曲線 \(x^2-y^2=a\) 上の点 \((x_{1},y_{1})\) における接線の方程式は
\(x_{1}x-y_{1}y=a\)
解答・解説
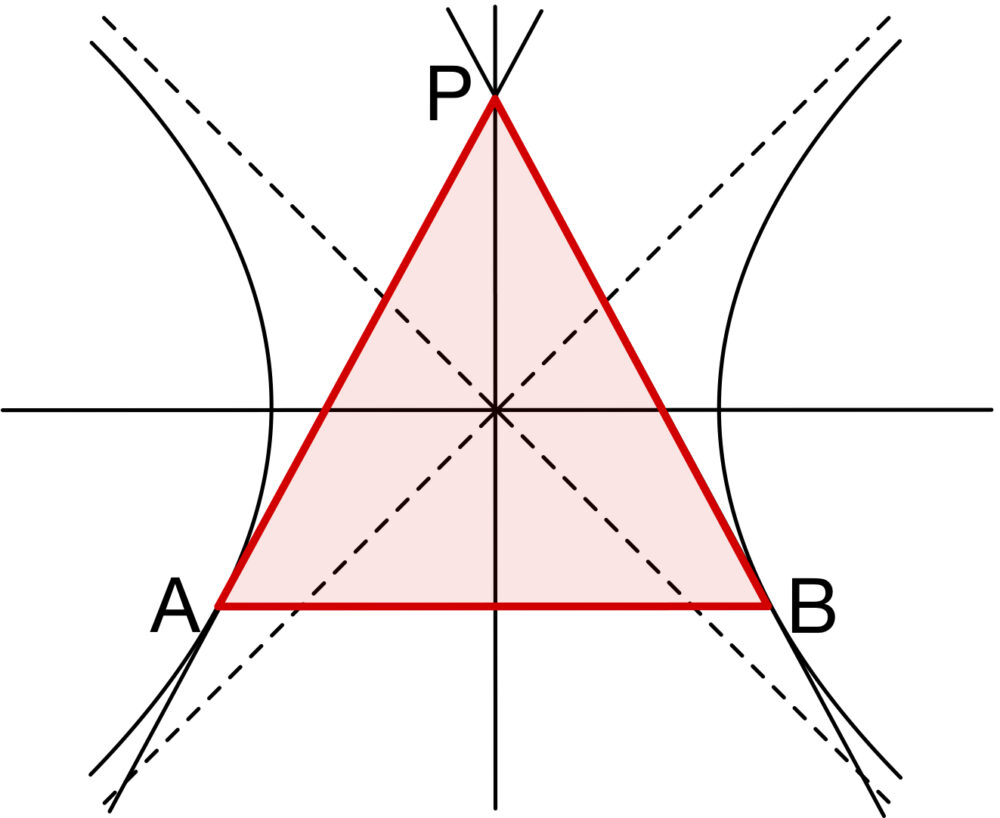 双曲線 \(x^2-y^2=1\) 上の点 \((x_{1},y_{1})\) における接線の方程式は
双曲線 \(x^2-y^2=1\) 上の点 \((x_{1},y_{1})\) における接線の方程式は
\(x_{1}x-y_{1}y=1\) ・・・①
①が \(P(0,p)\) を通るとき \(-y_{1}p=1\)
\(p>0\) より \(y_{1}=-\displaystyle\frac{1}{p}\) ・・・②
また,点 \((x_{1},y_{1})\) は双曲線 \(x^2-y^2=1\) 上より
\(x_{1}^2-y_{1}^2=1\) ・・・③
②を③に代入すると
\(x_{1}^2-\displaystyle\frac{1}{p^2}=1\)
\(x_{1}=\pm\sqrt{1+\displaystyle\frac{1}{p^2}}\)
よって,\(A\left(-\sqrt{1+\displaystyle\frac{1}{p^2}},-\displaystyle\frac{1}{p}\right)\),\(B\left(\sqrt{1+\displaystyle\frac{1}{p^2}},-\displaystyle\frac{1}{p}\right)\)
ゆえに \(\triangle PAB\) の面積を \(S\) とすると
\(S=\displaystyle\frac{1}{2}\cdot 2\sqrt{1+\displaystyle\frac{1}{p^2}}\cdot\left(p+\displaystyle\frac{1}{p}\right)=\displaystyle\frac{(p^2+1)^\frac{3}{2}}{p^2}\)

この式を微分して最小値を求めても構いませんが,やや計算が複雑に・・・。
そこで適切な置き換え・変形を行い,計算を楽にする一工夫を!
ここで,\(t=p^2\) ( \(t>0\) ) とおくと
\(S=\displaystyle\frac{(t+1)^\frac{3}{2}}{t}\)
\(f(t)=S^2=\displaystyle\frac{(t+1)^3}{t^2}\) とおく
\(f^{\prime}(t)=\displaystyle\frac{3(t+1)^2\cdot t^2-(t+1)^3\cdot 2t}{t^4}=\displaystyle\frac{(t+1)^2(t-2)}{t^3}\)
| \(t\) | \(0\) | \(2\) | ||
| \(f^{\prime}(t)\) | ー | \(0\) | + | |
| \(f(t)\) | ↘️ | (最小) | ↗️ |
\(t=2\) で \(S^2\) は最小値
つまり,\(p^2=2\)
\(p>0\) より \(p=\sqrt{2}\) のとき \(S\) は最小となる.







コメント