【2022神戸大学・理系・第4問】
\(a\) を正の実数とし,双曲線 \(\displaystyle\frac{x^2}{4}-\displaystyle\frac{y^2}{4}=1\) と直線 \(y=\sqrt{a}x+\sqrt{a}\) が異なる \(2\) 点 \(P\),\(Q\) で交わっているとする.線分 \(PQ\) の中点を \(R(s,t)\) とする.以下の問に答えよ.
(1) \(a\) のとりうる値の範囲を求めよ.
(2) \(s\),\(t\) の値を \(a\) を用いて表せ.
(3) \(a\) が(1)で求めた範囲を動くときに \(s\) のとりうる値の範囲を求めよ.
(4) \(t\) の値を \(s\) を用いて表せ.
解答・解説
(1) \(a\) のとりうる値の範囲
双曲線 \(\displaystyle\frac{x^2}{4}-\displaystyle\frac{y^2}{4}=1\) と直線 \(y=\sqrt{a}x+\sqrt{a}\) が異なる \(2\) 点で交わるので
\(\displaystyle\frac{x^2}{4}-\displaystyle\frac{\left(\sqrt{a}x+\sqrt{a}\right)^2}{4}=1\)
\(\iff\) \((1-a)x^2-2ax-a-4=0\) ・・・①
①が異なる \(2\) 実解を持てばよい.
よって \(a\not=1\) であり,このときに①の判別式を \(D\) とすると
\(\displaystyle\frac{D}{4}=(-a)^2+(1-a)(a+4)=-3a+4>0\)
したがって,\(a<\displaystyle\frac{4}{3}\)
\(a>0\),\(a\not=1\) より求める値の範囲は,
\(0<a<1\),\(1<a<\displaystyle\frac{4}{3}\)
(2) \(s\),\(t\) の値を \(a\) を用いて表せ.
①の異なる \(2\) つの実数解を \(\alpha\),\(\beta\) とすると,これらは点 \(P\),\(Q\) の \(x\) 座標となる.
解と係数の関係より
\(\alpha+\beta=\displaystyle\frac{2a}{1-a}\)
が成り立つので,線分 \(PQ\) の中点 \(R\) の \(x\) 座標は
\(s=\displaystyle\frac{\alpha+\beta}{2}=\displaystyle\frac{a}{1-a}\)
また,直線 \(y=\sqrt{a}x+\sqrt{a}\) 上に点 \(R(s,t)\) はあるので,
\(t=\sqrt{a}s+\sqrt{a}=\sqrt{a}\cdot\displaystyle\frac{a}{1-a}+\sqrt{a}=\displaystyle\frac{\sqrt{a}}{1-a}\)
したがって,\(s=\displaystyle\frac{a}{1-a}\),\(t=\displaystyle\frac{\sqrt{a}}{1-a}\)
(3) (1)のとき, \(s\) のとりうる値の範囲
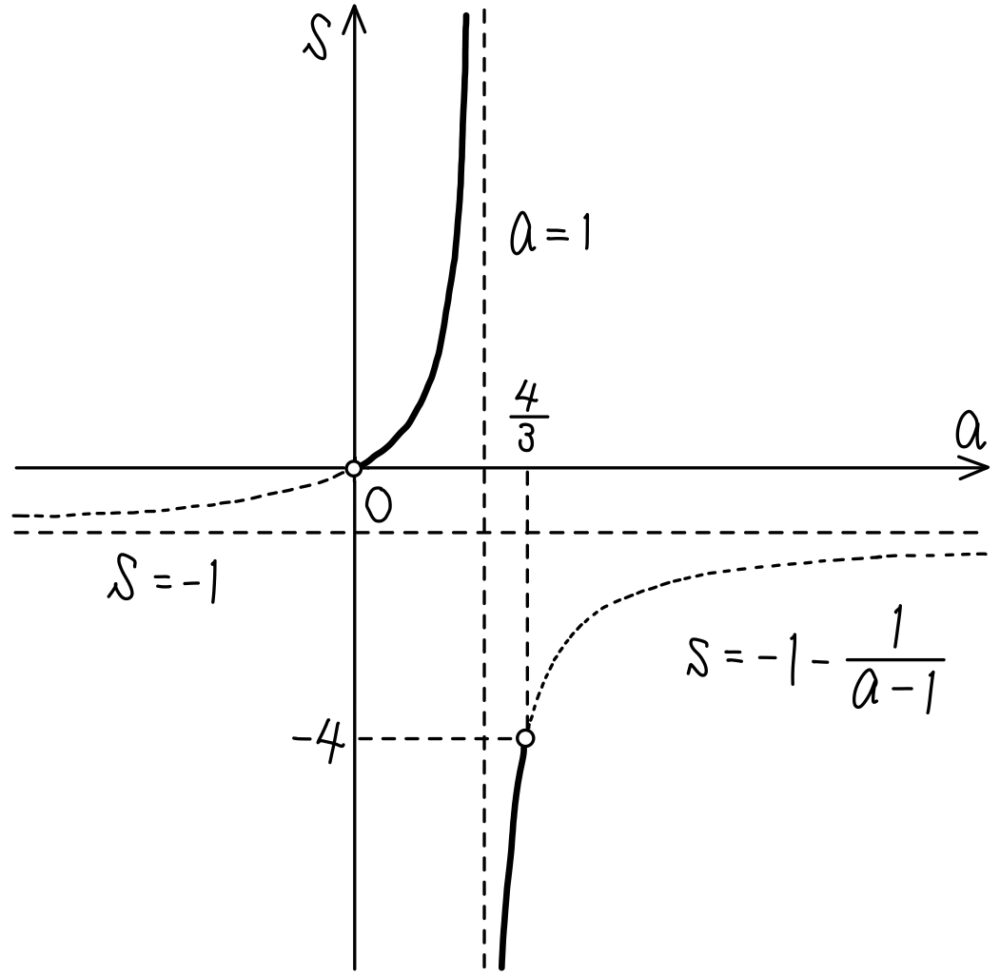 \(s=\displaystyle\frac{a}{1-a}=-1-\displaystyle\frac{1}{a-1}\) より
\(s=\displaystyle\frac{a}{1-a}=-1-\displaystyle\frac{1}{a-1}\) より
\(0<a<1\),\(1<a<\displaystyle\frac{4}{3}\) の範囲で
\(s=-1-\displaystyle\frac{1}{a-1}\) のグラフは右図のようになるので,
したがって,\(s\) のとりうる値の範囲は,\(s<-4\),\(0<s\)
(4) \(t\) の値を \(s\) を用いて表せ.
\(s=\displaystyle\frac{a}{1-a}\) より
\(s-sa=a\)
\(a(1+s)=s\)
(3)より \(s\not=-1\) より
よって,\(a=\displaystyle\frac{s}{1+s}\)
(2)より \(t=\displaystyle\frac{\sqrt{a}}{1-a}\) に代入すると
\(t=\displaystyle\frac{\sqrt{\displaystyle\frac{s}{1+s}}}{1-\displaystyle\frac{s}{1+s}}\)
\(t=(1+s)\sqrt{\displaystyle\frac{s}{1+s}}\)








コメント