【例題】
曲線 \(C\):\(y=x^3-4x\) 上の点 \(1,-3\) における接線 \(L\):\(y=-x-2\) となる.
このとき,曲線 \(C\) と接線 \(L\) の交点を求めよ.

\(2\) 曲線の交点でだから,連立して解けばいいだけですよね??
簡単ですよ!

もちろんその解き方が一般的ですね!
ただここでは,「変曲点」を利用した,マーク形式の試験(共通テストや私大受験)で使える裏技公式を紹介します!
実はこの問題であれば,\(10\) 秒くらいで答えが求まります!時間短縮の裏技としてマスターしましょう!
変曲点で知っておきたいPoint

そもそも「変曲点」とは何ですか?

上に凸と下に凸が入れ替わる点のことを言います。
数学Ⅲの微分で学習する内容になりますが,\(3\) 次関数の変曲点に関する性質は覚えておいて損はないので知っておいてください!
\(3\) 次関数の変曲点でおさえておきたい性質
① 変曲点の \(x\) 座標は,\(f^{\prime\prime}(x)=0\) を満たす \(x\)
例:\(y=x^3-4x\) のとき
\(y^{\prime}=3x^2\) ,\(y^{\prime\prime}=6x\) より
\(y^{\prime\prime}=0\) のとき,つまり \(x=0\) で変曲点を取ることがわかる.
② 極大点と極小点の中点になる
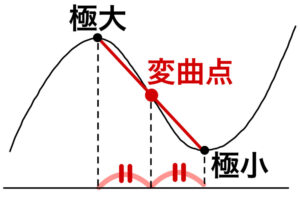
③ (交点〜変曲点):(変曲点〜接点) = 2:1
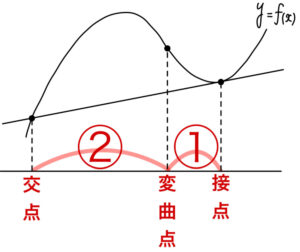
②については,\(3\) 次関数の対称性について証明問題としてもよく出題されます。
\(2\) 次試験で数学を使う人,余力がある人は是非おさえておきましょう!⏬
また,②の性質を利用した入試問題演習も是非!⏬

裏技をつかった解答
\(y=x^3-4x\) のとき
\(y^{\prime}=3x^2\) ,\(y^{\prime\prime}=6x\) より
\(y^{\prime\prime}=0\) のとき,つまり \(x=0\) で変曲点
また, \(x=1\) で接点であるから下図のような位置関係となる.
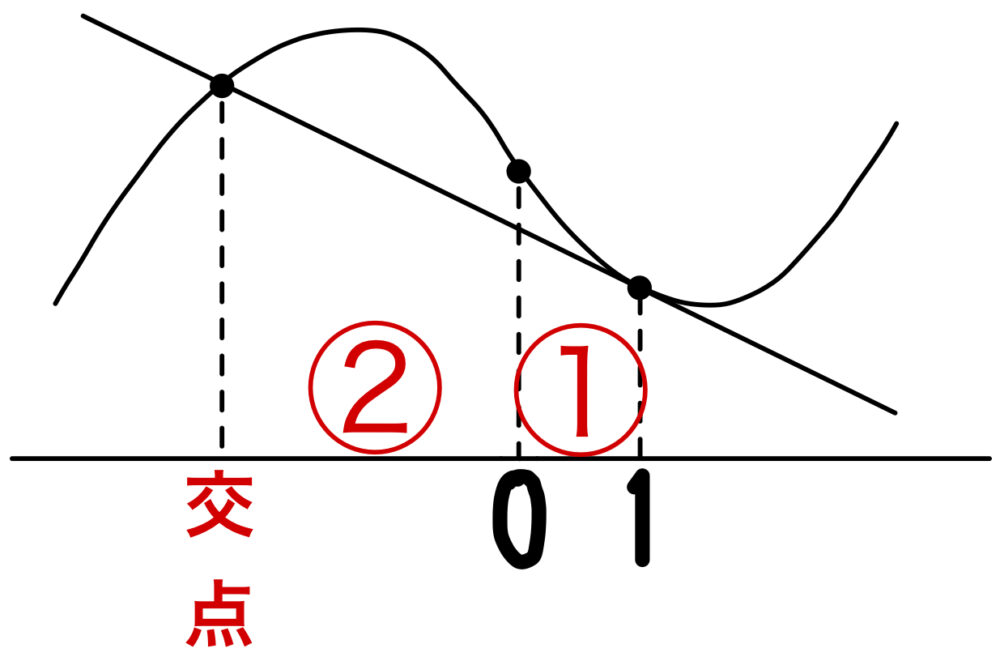
比が2:1になることに注目すると,交点の \(x\) 座標は \(x=-2\) であるとわかる.
よって接点でない交点は, \((-2,0)\) となる.







コメント