【2024立命館大学(全学統一2/2)・文系・第３問】
一方の面が白，他方の面が黒く塗られたカードが \(4\) 枚机の上にある．\(4\) 枚のカードのうち \(2\) 枚は表の面(見えている面)が白，残り \(2\) 枚は表の面が黒である．\(4\) 枚のカードのうち \(2\) 枚のカードを無作為に選び裏返す．これを \(1\) 回の試行とする．
この試行を \(n\) 回繰り返したとき，表の面が白であるカードと黒であるカードが \(2\) 枚ずつとなる確率を \(a_{n}\)，表の面がすべて白となる確率を \(b_{n}\)，表の面がすべて黒となる確率を \(c_{n}\) とする．このとき，次の問いに答えよ．
(１)\(a_{1}\)，\(b_{1}\)，\(c_{1}\) を求めよ．
(２)\(a_{2}\)，\(b_{2}\)，\(c_{2}\) を求めよ．
(３)\(a_{n+1}\) を \(a_{n}\) で表せ．
(４)\(a_{n}\) を求めよ．
確率漸化式・考え方・例題
解答・解説
(１) \(a_{1}\)，\(b_{1}\)，\(c_{1}\) を求めよ．
\(1\) 回の試行で白，黒が \(2\) 枚ずつとなるのは，
白と黒を \(1\) 枚ずつ選び，それらを裏返すとき
よって，\(a_{1}=\displaystyle\frac{_{2}C_{1}\cdot_{2}C_{1}}{_{4}C_{2}}=\displaystyle\frac{4}{6}=\displaystyle\frac{2}{3}\)
\(1\) 回の試行ですべてが白となるのは，黒を \(2\) 枚選び，それを裏返すとき
よって，\(b_{1}=\displaystyle\frac{_{2}C_{2}}{_{4}C_{2}}=\displaystyle\frac{1}{6}\)
\(c_{1}\) についても \(b_{1}\) と同様に考え，\(c_{1}=\displaystyle\frac{1}{6}\)
(２) \(a_{2}\)，\(b_{2}\)，\(c_{2}\) を求めよ．
\(n\) 回目と \(n+1\) 回目の状況の推移について考える．
・\(n+1\) 回目に白，黒が \(2\) 枚ずつ( \(a_{n+1}\) ) となるのは，
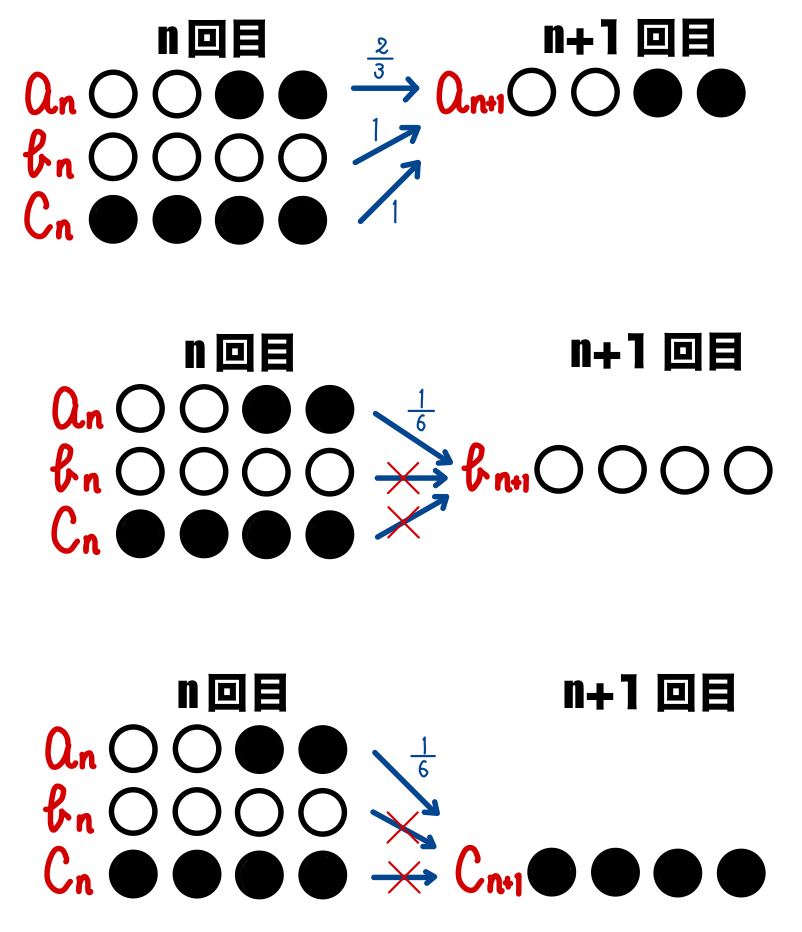\(n\) 回目に
①白黒が\(2\) 枚ずつ ( \(a_{n}\) ) のとき
白と黒を \(1\) 枚ずつ選び，それらを裏返す
このときの確率は(１)より \(\displaystyle\frac{2}{3}\)
②すべて白 ( \(b_{n}\) ) のとき
どの \(2\) 枚を選んで裏返してもよい
③すべて黒 ( \(c_{n}\) ) のとき
どの \(2\) 枚を選んで裏返してもよい
①～③より
\(a_{n+1}=\displaystyle\frac{2}{3}a_{n}+b_{n}+c_{n}\) ・・・④
次に
・\(n+1\) 回目にすべて白 ( \(b_{n+1}\) ) となるのは，
\(n\) 回目に白黒が\(2\) 枚ずつ ( \(a_{n}\) ) で
黒 \(2\) 枚を選び，それらを裏返すときのみ
よって，\(b_{n+1}=\displaystyle\frac{1}{6}a_{n}\)
・\(n+1\) 回目にすべて黒 ( \(c_{n+1}\) ) となるのは，
上と同様に考え，\(c_{n+1}=\displaystyle\frac{1}{6}a_{n}\)
以上より，
\(a_{2}=\displaystyle\frac{2}{3}a_{1}+b_{1}+c_{1}=\displaystyle\frac{7}{9}\)
\(b_{2}=\displaystyle\frac{1}{6}a_{1}=\displaystyle\frac{1}{9}\)
\(c_{2}=\displaystyle\frac{1}{6}a_{1}=\displaystyle\frac{1}{9}\)
(３) \(a_{n+1}\) を \(a_{n}\) で表せ．
\(a_{n}+b_{n}+c_{n}=1\) より，\( b_{n}+c_{n}=1- a_{n}\)
これを④に代入すると
\(a_{n+1}=\displaystyle\frac{2}{3}a_{n}+1-a_{n}\)
よって，\(a_{n+1}=-\displaystyle\frac{1}{3}a_{n}+1\) ・・・⑤
(４) \(a_{n}\) を求めよ．
⑤より
\(a_{n+1}-\displaystyle\frac{3}{4}=-\displaystyle\frac{1}{3}\left(a_{n}-\displaystyle\frac{3}{4}\right)\) と式変形できるので、
数列 \(\left\{a_{n}-\displaystyle\frac{3}{4}\right\}\) は初項が \(a_{1}-\displaystyle\frac{3}{4}=-\displaystyle\frac{1}{12}\) ，公比が \(-\displaystyle\frac{1}{3}\) の等比数列となるから
\(a_{n+1}-\displaystyle\frac{3}{4}=-\displaystyle\frac{1}{12}\left(-\displaystyle\frac{1}{3}\right)^{n-1}\)
したがって，\(a_{n}=\displaystyle\frac{1}{4}\left\{3+\left(-\displaystyle\frac{1}{3}\right)^n\right\}\)
コメント