【2013大阪大学】三角関数の極限x→0のときsinx/x=1、sinxの導関数の証明

\(\displaystyle\lim_{x\rightarrow 0}\displaystyle\frac{\sin x}{x}=1\) の証明

( ⅰ )　\(0<x<\displaystyle\frac{\pi}{2}\) のとき

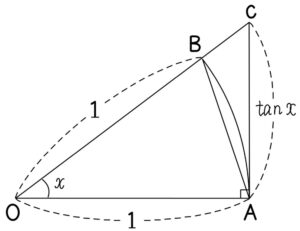
半径 \(1\) , 中心角 \(\angle AOB=x\) の扇形 \(OAB\) の面積を \(S\) , 点 \(A\) を通り \(OA\) に垂直な直線と，直線 \(OB\) の交点を \(C\) とする．

このとき，\(\triangle OAB<S<\triangle OAC\) より

\(\displaystyle\frac{1}{2}\cdot1\cdot1\cdot\sin x<\displaystyle\frac{1}{2}\cdot1^2\cdot x<\displaystyle\frac{1}{2}\cdot1\cdot \tan x\)

よって，\(\sin x<x<\tan x\) ・・・①

\(0<x<\displaystyle\frac{\pi}{2}\) のとき \(\sin x>0\) であるから，①の各辺を \(\sin x\) で割ると

\(1<\displaystyle\frac{x}{\sin x}<\displaystyle\frac{\tan x}{\sin x}=\displaystyle\frac{1}{\cos x}\)

逆数をとると

\(\cos x<\displaystyle\frac{\sin x}{x}<1\)

\(\displaystyle\lim_{x\rightarrow +0}\cos x=1\) であるから，はさみうちの原理より

\(\displaystyle\lim_{x\rightarrow +0}\displaystyle\frac{\sin x}{x}=1\)

( ⅱ )　\(-\displaystyle\frac{\pi}{2}<x<0\) のとき

\(x=-\theta\) とおくと

\(\displaystyle\lim_{x\rightarrow -0}\displaystyle\frac{\sin x}{x}=\displaystyle\lim_{\theta\rightarrow +0}\displaystyle\frac{\sin (-\theta)}{-θ}=\displaystyle\lim_{\theta\rightarrow +0}\displaystyle\frac{\sin \theta}{\theta}=1\)

( ⅰ )，( ⅱ )より \(\displaystyle\lim_{x\rightarrow 0}\displaystyle\frac{\sin x}{x}=1\)

\(\sin x\) の導関数の証明

\((\sin x)^{\prime}=\displaystyle\lim_{h\rightarrow 0}\displaystyle\frac{\sin(x+h)-\sin x}{h}\)

和積の公式より（和積の公式が不安な方はこちら）

\((\sin x)^{\prime}=\displaystyle\lim_{h\rightarrow 0}\displaystyle\frac{2\cos\left(x+\displaystyle\frac{h}{2}\right)\sin \displaystyle\frac{h}{2}}{h}\)

\(=\displaystyle\lim_{h\rightarrow 0}\displaystyle\frac{\sin \displaystyle\frac{h}{2}}{\displaystyle\frac{h}{2}}\cdot\cos\left(x+\displaystyle\frac{h}{2}\right)=\cos x\)