【2022京都大学(理系:第4問、文系:第5問)】

確認事項
\(2\) つのベクトルが垂直であるとき、内積が \(0\)
\(3\) 点が一直線上
\(△ABC\) の重心 \(G\) について
\(\overrightarrow{OG}=\displaystyle\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})\)
\(O\) を \(A\) とすると、
\(\overrightarrow{AG}=\displaystyle\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})\)
解答
(1)
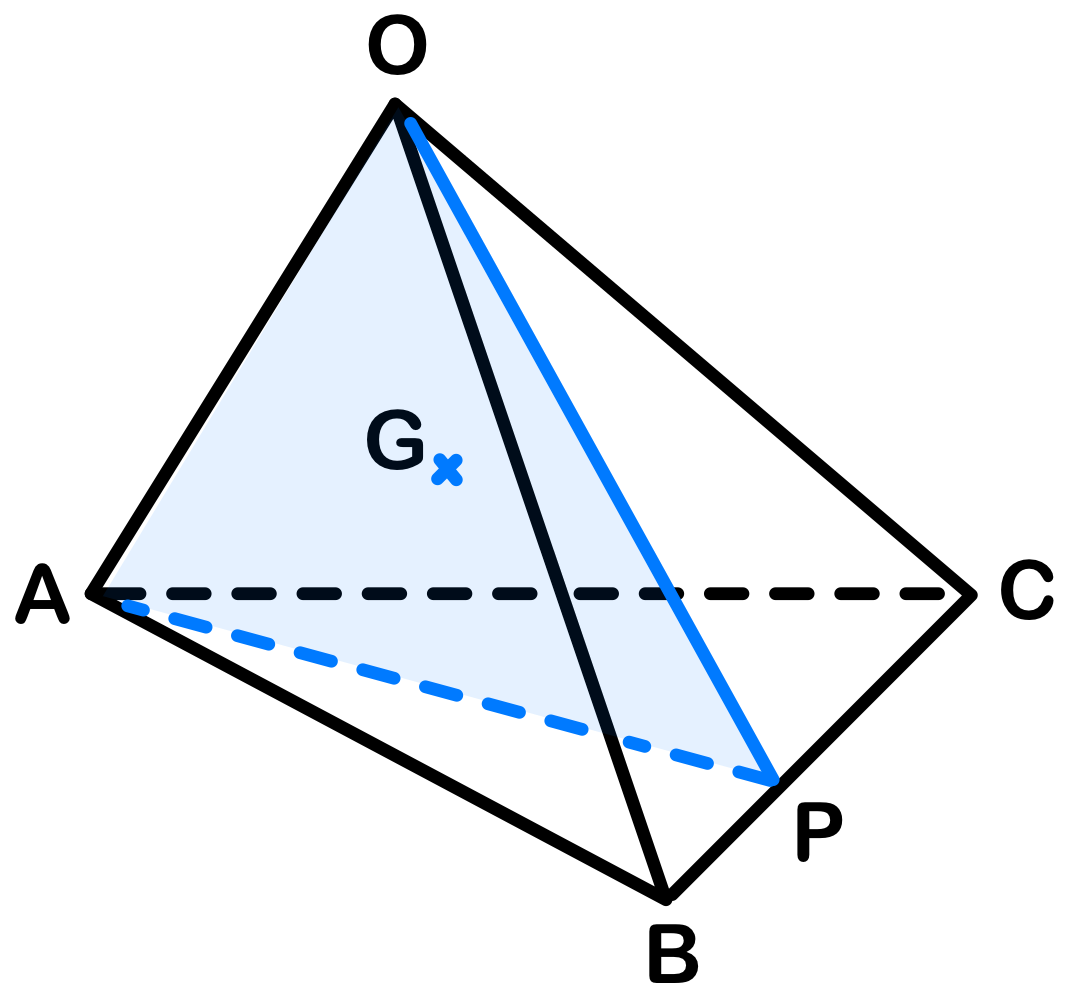
\(\overrightarrow{OA}=\overrightarrow{a}\)、\(\overrightarrow{OB}=\overrightarrow{b}\)、\(\overrightarrow{OC}=\overrightarrow{c}\)、\(\overrightarrow{OP}=\overrightarrow{p}\)、\(\overrightarrow{OG}=\overrightarrow{g}\) とおく.
点 \(P\) は \(BC\) 上より、実数 \(t\) を用いて、
\(\overrightarrow{BP}=t\overrightarrow{BC}\) とおけ、
\(\overrightarrow{p}-\overrightarrow{b}=t(\overrightarrow{c}-\overrightarrow{b})\)
よって、\(\overrightarrow{p}=(1-t)\overrightarrow{b}+t\overrightarrow{c}\) ・・・①
また、点 \(G\) は \(△OAP\) の重心であるから、
\(\overrightarrow{g}=\displaystyle\frac{1}{3}(\overrightarrow{a}+\overrightarrow{p})\)
よって、\(\overrightarrow{PG}=\overrightarrow{g}-\overrightarrow{p}=\displaystyle\frac{1}{3}(\overrightarrow{a}-2\overrightarrow{p})\) ・・・②
②より、\(\overrightarrow{PG}\cdot\overrightarrow{a}=\displaystyle\frac{1}{3}(|\overrightarrow{a}|^2-2\overrightarrow{a}\cdot\overrightarrow{p})\) ・・・③
①より、
\(\overrightarrow{a}\cdot\overrightarrow{p}=(1-t)\overrightarrow{a}\cdot\overrightarrow{b}+t\overrightarrow{a}\cdot\overrightarrow{c}\) ・・・④
ここで、\(\overrightarrow{a}\cdot\overrightarrow{b}\)、\(\overrightarrow{a}\cdot\overrightarrow{c}\) の値について考える.
\(△OAB\) において、
\(|\overrightarrow{AB}|=3 \iff |\overrightarrow{b}-\overrightarrow{a}|=3\) を \(2\) 乗すると、
\(|\overrightarrow{b}|^2-2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{a}|^2=9\)
\(|\overrightarrow{a}|=4\)、\(|\overrightarrow{b}|=3\) より
\(\overrightarrow{a}\cdot\overrightarrow{b}=8\)
同様に考え、\(\overrightarrow{a}\cdot\overrightarrow{c}=8\)
よって④より、\(\overrightarrow{a}\cdot\overrightarrow{p}=8\) となるので、③に代入すると、
\(\overrightarrow{PG}\cdot\overrightarrow{a}=\displaystyle\frac{1}{3}(4^2-2\times8)=0\)
したがって、\(\overrightarrow{PG}\perp\overrightarrow{OA}\)
(2)
②より、\(|\overrightarrow{PG}|^2=\displaystyle\frac{1}{9}(|\overrightarrow{a}|^2-4\overrightarrow{a}\cdot\overrightarrow{p}+4|\overrightarrow{p}|^2)\)
\(|\overrightarrow{a}|=4\)、\(\overrightarrow{a}\cdot\overrightarrow{p}=8\) より、
\(|\overrightarrow{PG}|^2=\displaystyle\frac{4}{9}(|\overrightarrow{p}|^2-4)\)
したがって、\(|\overrightarrow{p}|\) が最小となるとき \(|\overrightarrow{PG}|\) が最小となる.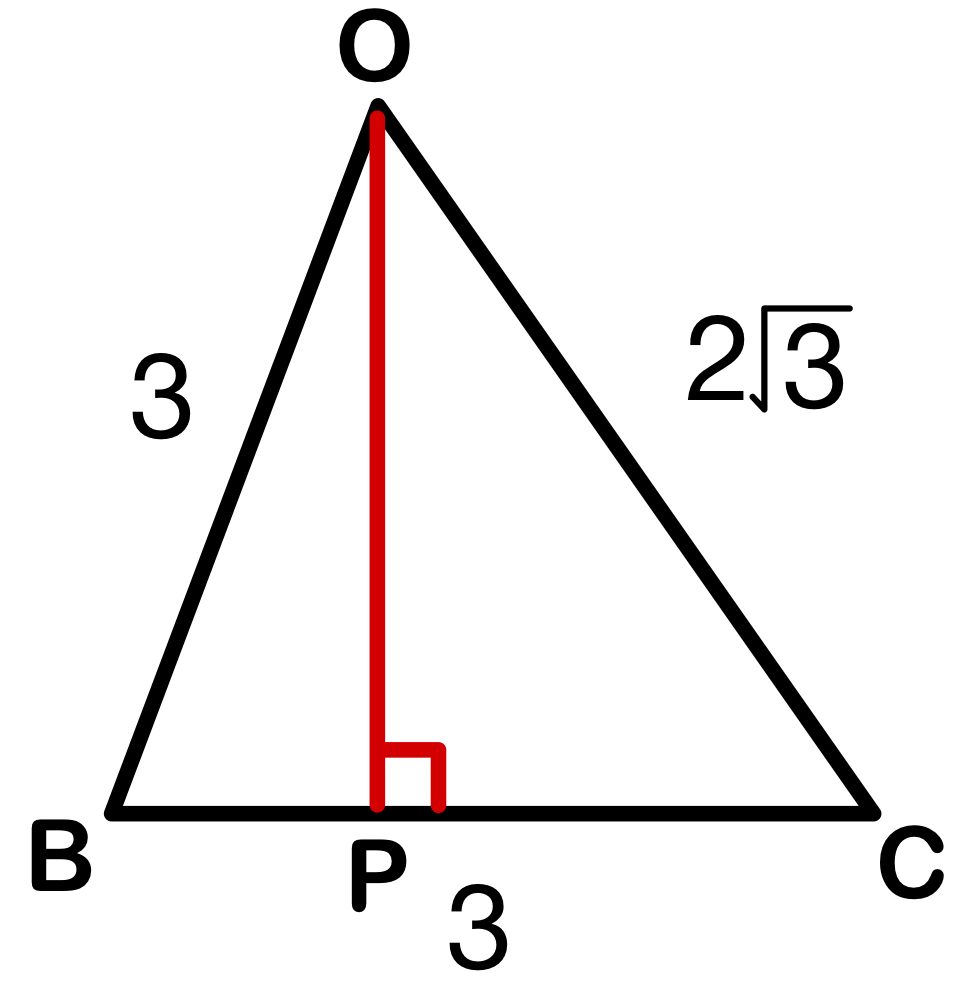
つまり、点 \(O\) から \(BC\) への距離が最小となればよいので、\(OP\perp BC\) のときである.
余弦定理より、\(\cos\angle OBC=\displaystyle\frac{3^2+3^2-(2\sqrt3)^2}{2\cdot 2\cdot 3}=\displaystyle\frac{1}{3}\) であり、
\(△OBP\) に注目して、
\(\cos\angle OBC=\displaystyle\frac{BP}{OB}\) より、\(BP=1\)
よって、\(OP=2\sqrt{2}\)
このとき、
\(|\overrightarrow{PG}|^2=\displaystyle\frac{4}{9}((2\sqrt{2})^2-4)=\displaystyle\frac{16}{9}\) なので、
求める最小値は、\(PG=\displaystyle\frac{4}{3}\)







コメント
対称面を見つけたら座標で置くという定石に則り、O(0,0,0), A(0,0,4), B(2,1,2), C(2,-2,2)と置くと瞬殺
コメント・マスマス学ぶをご覧いただき誠にありがとうございます。
とても優秀な方の解法ですね ♪確かに簡潔な解答が作成できそうです!
他の問題でも対称性については扱っていますが、対称性を利用して考えることは非常に重要な考え方です!また、空間ベクトルの問題を座標に落として考えるという発想も、受験数学においてはとても重要な考え方ですね!
しかしここでは、多くの方が読んでいただき、まだベクトルを学習したばっかりの読者もおります。そこでまずはオーソドックスな解法を紹介させていただきました。(京都大学という難関大学でも、基本的なことの組み合わせだけで解けるということをお伝えしたいという目的がありました。)そのような意図のもと今回の解法を紹介させていただきました。
しかし「2022受験者様」のように優秀な読者もいていただけるということを分かりましたので、今後はより発展的な内容の記事も紹介できるようにさせていただきます。
数学は様々な考え、アプローチによって解法がたくさんあります。その解法を考えること(仮に答えに辿り着かなくても)に意味があり、数学の面白さだと私は思っています。
このようにコメントをいただき、素敵な別解を紹介していただけたことは大変嬉しく思います。
まだまだ不慣れなブログ運営で、誤字やミス等もあるかもしれませんが、頑張る受験生に少しでもお役に立てるように今後ともコツコツと活動していきますので、これからもまた一読者としてご意見等いただけると幸いです。
今回はコメントありがとうございました。