【2021数学ⅡB(第１日程)】第２問(微分法・積分法)
(１)問題と解答・解説《ア〜キ》
解答・解説《ア〜キ》
①，②の共通点について
\(y\) 軸との交点の \(y\) 座標は，\(x=0\) として \(y=0\) ・・・《ア》
①から \(y^{\prime}=6x+2\) ，②から \(y^{\prime}=4x+2\) より \(x=0\) における接線の傾きは \(2\)
よって，\(y\) 軸との交点 \((0,3)\) における接線の方程式は，
\(y=2x+3\) ・・・《イウ》
\(y\) 軸との交点における接線が \(y=2x+3\) のとき，
\((0,3)\) を通り，\(x=0\) における微分係数(接線の傾き)が \(2\) となれば良いので，
それを満たすのは，④ \(y=-x^2+2x+3\) ・・・《エ》
次に，\(y=ax^2+bx+c\) 上の点 \((0,c)\) ・・・《オ》
における接線を \(l\) とすると
\(y^{\prime}=2ax+b\) より \(x=0\) のとき接線の傾きは \(b\)
よって，\(y=bx+c\) ・・・《カキ》
(１)問題と解答・解説《ク〜セ》
解答・解説《ク〜セ》
接線 \(l\) ：\(y=bx+c\) と \(x\) 軸との交点の \(x\) 座標は \(b\not=0\) より
\(x=\displaystyle\frac{-c}{b}\) ・・・《ク〜コ》
\(a\) , \(b\) , \(c\) が正の実数のとき
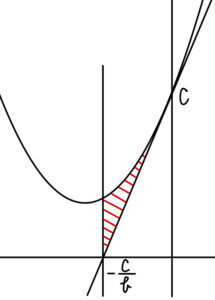曲線 \(y=ax^2+bx+c\) と接線 \(l\) および直線 \(x=-\displaystyle\frac{c}{b}\) で囲まれた図形の面積 \(S\) は，\(-\displaystyle\frac{c}{b}<0\) より
\(S=\displaystyle\int^{0}_{-\frac{c}{b}}\left\{(ax^2+bx+c)-(bx+c)\right\} dx\)
\(=\displaystyle\int^{0}_{-\frac{c}{b}}ax^2 dx\)
\(=\Bigl[\displaystyle\frac{a}{3}x^3\Bigr]^{0}_{-\frac{c}{b}}\)
\(=\displaystyle\frac{ac^3}{3b^3}\) ・・・《サ〜ス》
\(a=1\) のとき
\(S=\displaystyle\frac{c^3}{3b^3}=\displaystyle\frac{1}{3}\left(\displaystyle\frac{c}{b}\right)^3\)
が一定となるように \(b\) , \(c\) を変化させるとき
定数 \(k\) を用いて \(k=\displaystyle\frac{c}{b}\) \(\iff\) \(c=kb\)
よって \(b\) と \(c\) は比例の関係であるから，\(b\) と \(c\) の関係を表すグラフの概形は ⓪ ・・・《セ》
(２)問題と解答・解説《ソ〜ト》
解答・解説《ソ〜ト》
④，⑤，⑥のグラフにおいて \(x=0\) とすると \(y=5\) ・・・《ソ》
④より \(y^{\prime}=12x^2+4x+3\) , ⑤より \(y^{\prime}=-6x^2+14x+3\) , ⑥より \(y^{\prime}=15x^2-2x+3\) なので，\(x=0\) における接線の傾きはいずれも \(3\) となる．
よって， \(y\) 軸との交点 \((0,5)\) における接線の方程式は，
\(y=3x+5\) ・・・《タチ》
次に，\(y=ax^3+bx^2+cx+d\) 上の点 \((0,d)\) ・・・《ツ》における接線の方程式について
\(y^{\prime}=3ax^2+2bx+c\) より \(x=0\) における接線の傾きは \(c\) であるから，
求める接線の方程式は \(y=cx+d\) ・・・《テト》
(２)問題と解答・解説《ナ〜ホ》
解答・解説《ナ〜ホ》
\(h(x)=ax^3+bx^2\) について
\(h^{\prime}=3ax^2+2bx=3ax\left(x+\displaystyle\frac{2b}{3a}\right)\)
よって，\(a>0\) , \(b>0\) であるから，\(y=h(x)\) のグラフの増減表は以下のようになる．
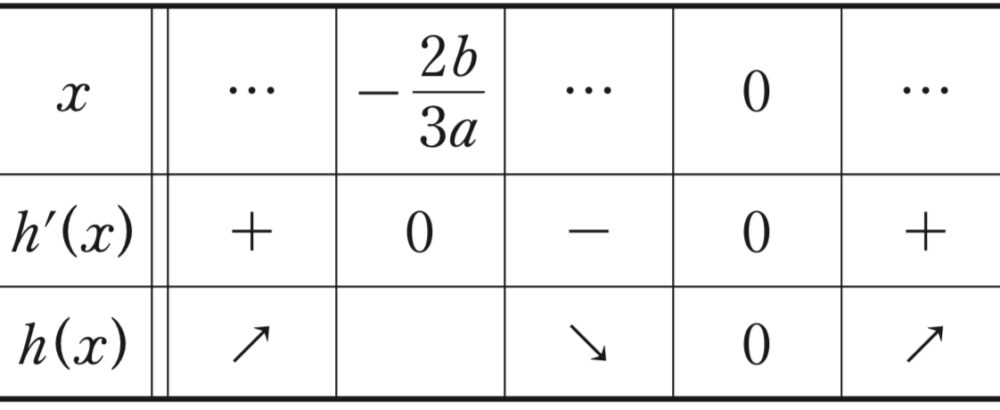
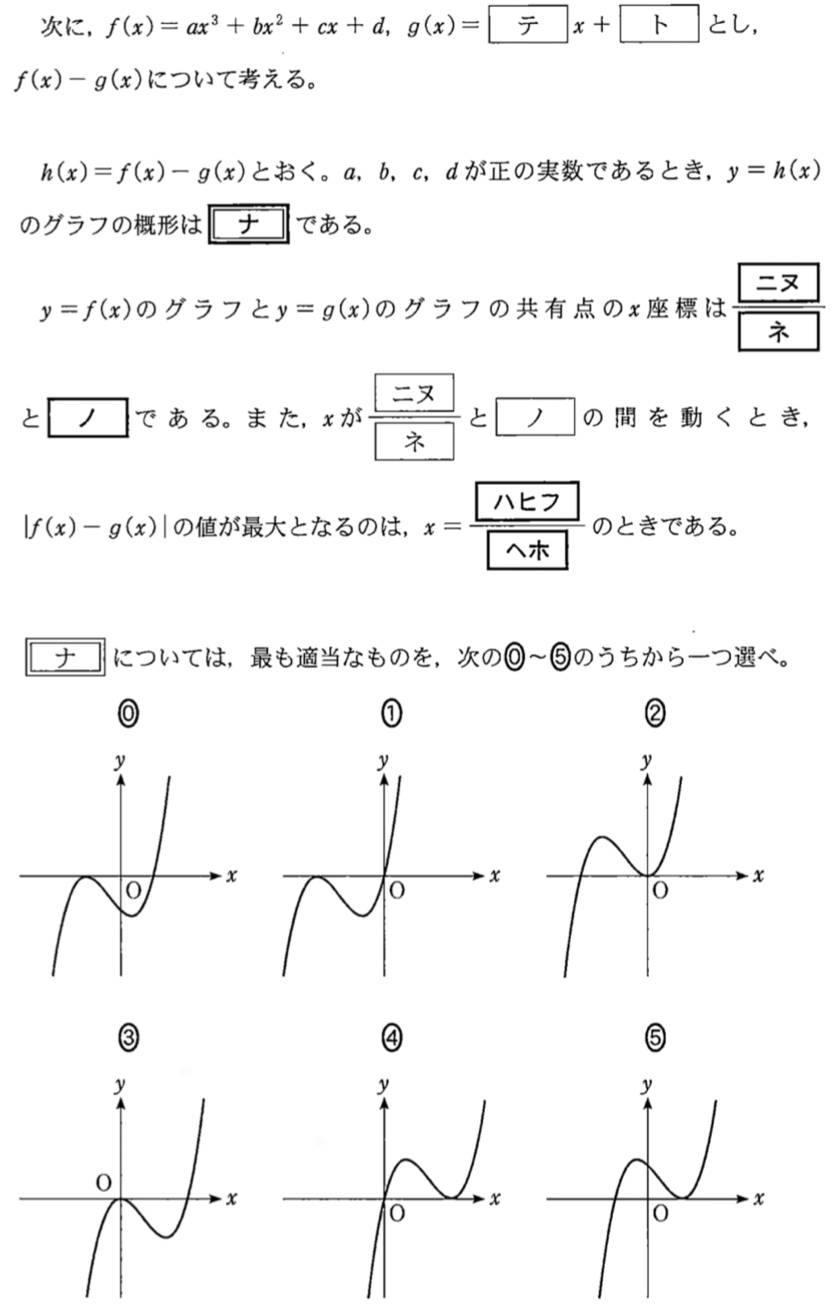
したがって，\(y=h(x)\) のグラフの概形は ② ・・・《ナ》
また，\(y=f(x)\) と \(y=g(x)\) の共有点の \(x\) 座標は
\(f(x)=g(x)\) \(\iff\) \(h(x)=0\) の方程式の解であるから，
\(ax^3+bx^2=0\) \(\iff\) \(ax^2\left(x+\displaystyle\frac{b}{a}\right)=0\)
よって，\(x = \displaystyle\frac{-b}{a} , 0\) ・・・《ニ〜ノ》
また，\(x\) が \(-\displaystyle\frac{b}{a}\) と \(0\) の間を動くとき，グラフの概形から \(h(x)>0\) となる．
\(|f(x)-g(x)|=|h(x)|=ax^3+bx^2\)
この値が最大となるのは，\(x=\displaystyle\frac{-2b}{3a}\) ・・・《ハ〜ホ》のとき
コメント