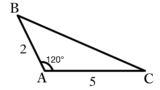
\([ あ ] AB^2+ [ い ] AC^2=AD^2+ [ う ] BD^2\)
が成り立つ.
平面図形へのアプローチ
おそらく多くの人が余弦定理を用いて計算を行ったのではないでしょうか?もちろん正解です!
ただここでお話ししたいことは、解けたかどうかではありません。(もちろん解けて欲しいですが・・・)
そもそも、どうしてこの問題を見て『幾何(三角比)』の問題だと思ったのでしょうか?
ベクトルや座標は頭の中に浮かびましたか??
ベクトルや座標を考慮した上で、幾何的に解くのが一番良いと判断したのであれば何も言うことはありません。
幾何の分野であると決めつけてしまったことに問題があります。
平面図形の問題 👉 3つのアプローチ!
①幾何(三角比・合同・相似など)
②座標
③ベクトル
(数Ⅲを履修している人は④複素平面 ⑤極座標など)それぞれの解法どの解法が良いとか悪いと言うことではありません。
まずはどれでも良いので解けることが大切。その上で、レベルアップをしたいのであればすべての解法が思いつくように!!
解答・解説(座標を利用)
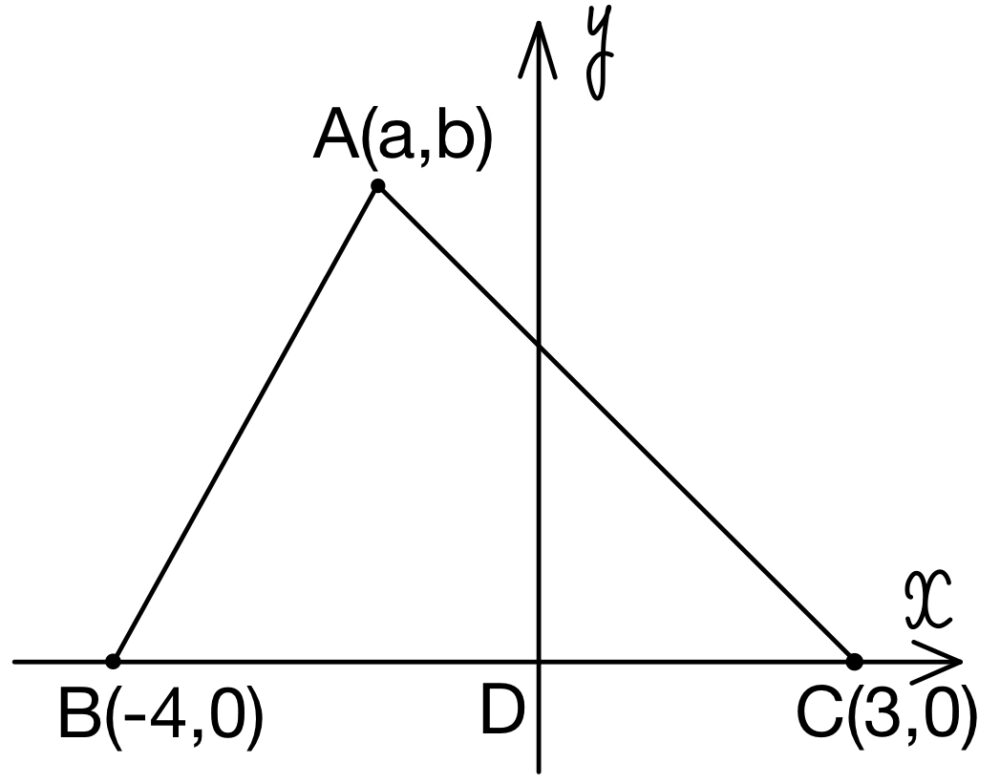 \(3\) 点 \(A\) , \(B\) , \(C\) を \(xy\) 座標平面上に
\(3\) 点 \(A\) , \(B\) , \(C\) を \(xy\) 座標平面上に
\(A(a,b)\),\(B(-4,0)\),\(C(3,0)\),\(D(0,0)\) ( ただし \(b\not=0\) ) とおいても一般性を失わない.
\(AB^2=(a+4)^2+b^2=a^2+8a+b^2+16\)
\(AC^2=(a-3)^2+b^2=a^2-6a+b^2+9\)
\(AD^2=a^2+b^2\)
\(BD^2=16\)
ここで,\(xAB^2+yAC^2=AD^2+zBD^2\) とおくと
\(x(a^2+8a+b^2+16)+y(a^2-6a+b^2+9)=a^2+b^2+16z\)
\((x+y)a^2+(8x-6y)a+(x+y)b^2+16x+9y=a^2+b^2+16z\)
これが任意の \(a\),\(b\) で成立するとき
\(\begin{cases}x+y=1\\8x-6y=0\\16x+9y=16z\end{cases}\)
よって \((x,y,z)=\left(\displaystyle\frac{3}{7},\displaystyle\frac{4}{7},\displaystyle\frac{3}{4}\right)\)
したがって,
\(\displaystyle\frac{3}{7}AB^2+\displaystyle\frac{4}{7}AC^2=AD^2+\displaystyle\frac{3}{4}BD^2\)

余弦定理を利用した解法でももちろんOK!
練習では様々な視点から問題にアプローチできる習慣を身につけることで,試験本番で真っ白答案を回避することができるようになります!







コメント