【2022北海道大学・理系(第5問)】
複素数 \(z\) に関する次の \(2\) つの方程式を考える.ただし,\(\overline{z}\) を \(z\) と共役な複素数とし, \(i\) を虚数単位とする.
\(z\overline{z}=4\) ・・・①,\(|z|=|z-\sqrt{3}+i|\) ・・・②
(1) ①,②それぞれの方程式について,その解 \(z\) 全体が表す図形を複素数平面上に図示せよ.
(2) ①,②の共通解となる複素数をすべて求めよ.
(3) (2)で求めたすべての複素数の積を \(w\) とおく.このとき, \(w^n\) が負の実数となるための整数 \(n\) の必要十分条件を求めよ.
解答・解説
(1)
\(z=x+yi\) ( \(x\),\(y\) は実数 ) とおくと,
\(z\overline{z}=4\) より
\((x+yi)(x-yi)=4\) \(\iff\) \(x^2+y^2=4\) ・・・① ’
\(|z|=|z-\sqrt{3}+i|\) より
\(|x+yi|=|x+yi-\sqrt{3}+i|=|(x-\sqrt{3})+(y+1)i|\)
\(\iff\) \(\sqrt{x^2+y^2}=\sqrt{(x-\sqrt{3})^2+(y+1)^2}\)
両辺を \(2\) 乗してまとめると
\(y=\sqrt{3}x-2\) ・・・② ‘
① ’,② ‘ の交点を求めると
\((x,y)=(0,-2),(\sqrt{3},1)\) より
\(z\) 全体が表す図形は下図となる.
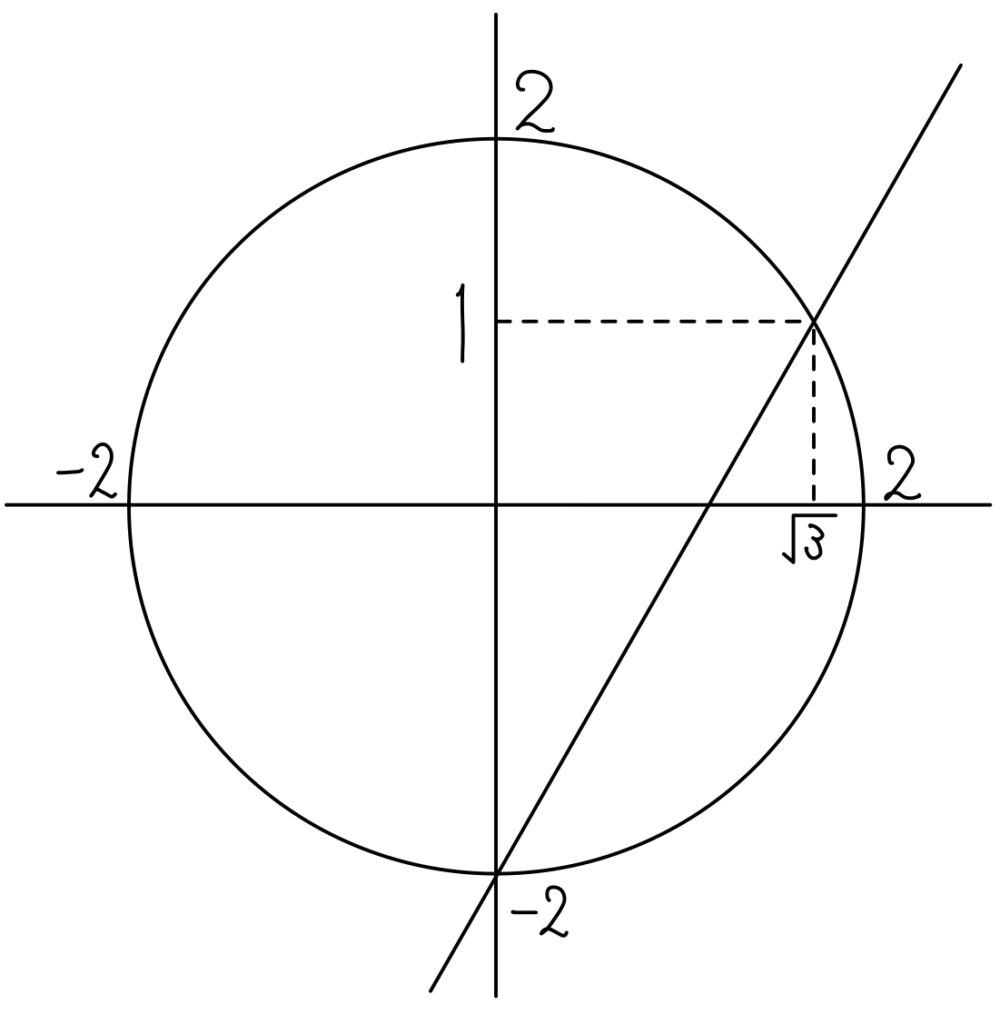
(2)
(1)より \(z=-2i\) ,\(z=\sqrt{3}+i\)
(3)
\(w=-2i(\sqrt{3}+i)=2-2\sqrt{3}i\) より
\(w=4\left\{-\cos\left(\displaystyle\frac{\pi}{3}\right)+i\sin\left(-\displaystyle\frac{\pi}{3}\right)\right\}\)
ド・モアブルの定理より
\(w^n=4^n\left\{\cos\left(-\displaystyle\frac{n\pi}{3}\right)+i\sin\left(-\displaystyle\frac{n\pi}{3}\right)\right\}\)
これが負の実数となるのは,整数 \(k\) を用いて
\(-\displaystyle\frac{n\pi}{3}=(2k-1)\pi\)
よって,\(n=-6k+3\) ( k は整数 )







コメント