【2023名古屋大学・理系・第1問】
実数係数の \(4\) 次方程式 \(x^4-px^3+qx^2-rx+s=0\) は相異なる複素数 \(\alpha\),\(\overline{\alpha}\),\(\beta\),\(\overline{\beta}\) を解に持ち,それらは全て複素数平面において,点 \(1\) を中心とする半径 \(1\) の円周上にあるとする.ただし,\(\overline{\alpha}\),\(\overline{\beta}\) はそれぞれ \(\alpha\),\(\beta\) と共役な複素数を表す.
(1) \(\alpha+\overline{\alpha}=\alpha\overline{\alpha}\) を示せ.
(2) \(t=\alpha+\overline{\alpha}\),\(u=\beta+\overline{\beta}\) とおく.\(p\),\(q\),\(r\),\(s\) をそれぞれ \(t\) と \(u\) で表せ.
(3) 座標平面において,点 \((p,s)\) のとりうる範囲を図示せよ.
解答・解説
(1) \(\alpha+\overline{\alpha}=\alpha\overline{\alpha}\) を示せ.
\(\alpha\) は点 \(1\) を中心とする半径 \(1\) の円周上にあるので
\(|\alpha-1|=1\)
\(2\) 乗すると \(|\alpha-1|^2=1\)
\((\alpha-1)(\overline{\alpha}-1)=1\)
\(\alpha\overline{\alpha}-\alpha-\overline{\alpha}+1=1\)
よって,\(\alpha+\overline{\alpha}=\alpha\overline{\alpha}\)
(2) \(p\),\(q\),\(r\),\(s\) をそれぞれ \(t\) と \(u\) で表せ.
(1)より,
\(\alpha+\overline{\alpha}=\alpha\overline{\alpha}=t\)
\(\beta+\overline{\beta}=\beta\overline{\beta}=u\) とおける.
\(4\) 次方程式 \(x^4-px^3+qx^2-rx+s=0\) は相異なる複素数 \(\alpha\),\(\overline{\alpha}\),\(\beta\),\(\overline{\beta}\) を解に持つので
\(x^4-px^3+qx^2-rx+s=(x-\alpha)(x-\overline{\alpha})(x-\beta)(x-\overline{\beta})\)
\(=(x^2-tx+t)(x^2-ux+u)\)
\(=x^4-(t+u)x^3+(tu+t+u)x^2-2tux+tu\)
それぞれの係数を比較すると
\(p=t+u\),\(q=tu+t+u\),\(r=2tu\),\(s=tu\)
(3) 座標平面において,点 \((p,s)\) のとりうる範囲を図示せよ.
\(\alpha\),\(\overline{\alpha}\),\(\beta\),\(\overline{\beta}\) はすべて異なるので
\(\alpha\),\(\beta\) はともに虚数解となるので,
\(x^2-tx+t=0\),\(x^2-ux+u=0\) のそれぞれの判別式を \(D_{1}\),\(D_{2}\) とおくと,
\(D_{1}<0\) かつ \(D_{2}<0\)
\(\iff\) \(t^2-4t<0\) かつ \(u^2-4u<0\)
\(\iff\) \(0<t<4\) かつ \(0<u<4\) ・・・①
ここで \(X=t,u\) を \(2\) 解にもつ \(2\) 次方程式は
\(X^2-(t+u)X+tu=0\)
(2)より \(X^2-pX+s=0\) ・・・②
①より,\(0<X<4\) に②が異なる \(2\) つの実数解を持てばよい.
\(f(X)=X^2-pX+s\) とおくとき,次の条件を満たせばよい.
・\(f(X)=0\) の判別式 \(D>0\)
・\(0<\) \(f(X)\) の軸 \(<4\)
・\(f(0)>0\)
・\(f(4)>0\)
それぞれ計算すると
\(p^2-4s>0\),\(0<\displaystyle\frac{p}{2}<4\),\(s>0\),\(16-4p+s>0\)
\(\iff\) \(s<\displaystyle\frac{p^2}{4}\),\(0<p<8\),\(s>0\),\(s>4p-16\)
したがって,点 \((p,s)\) のとりうる範囲は下図の斜線部分(ただし境界線は含まない)
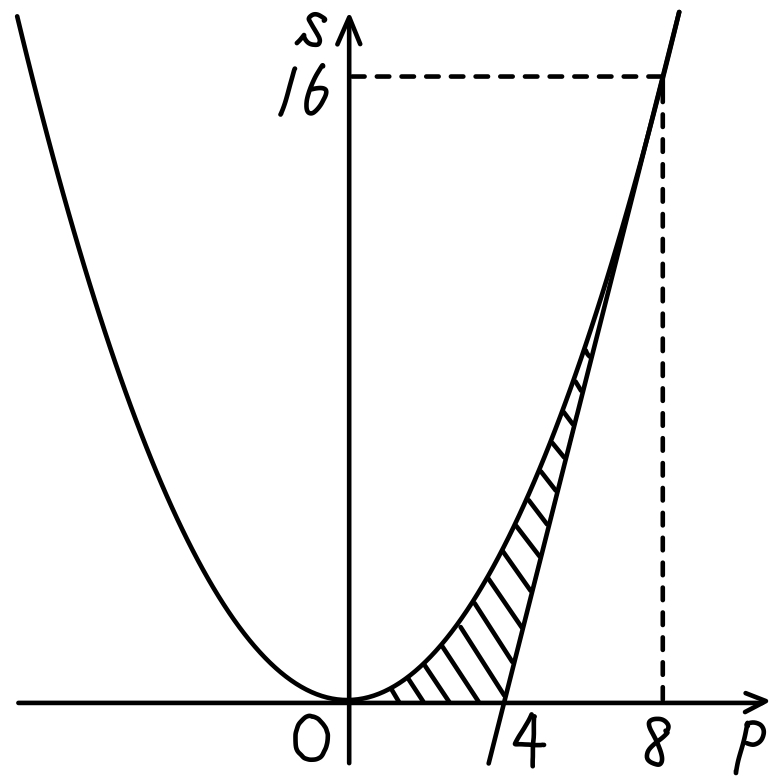







コメント