【2020大阪大学・第3問・文】
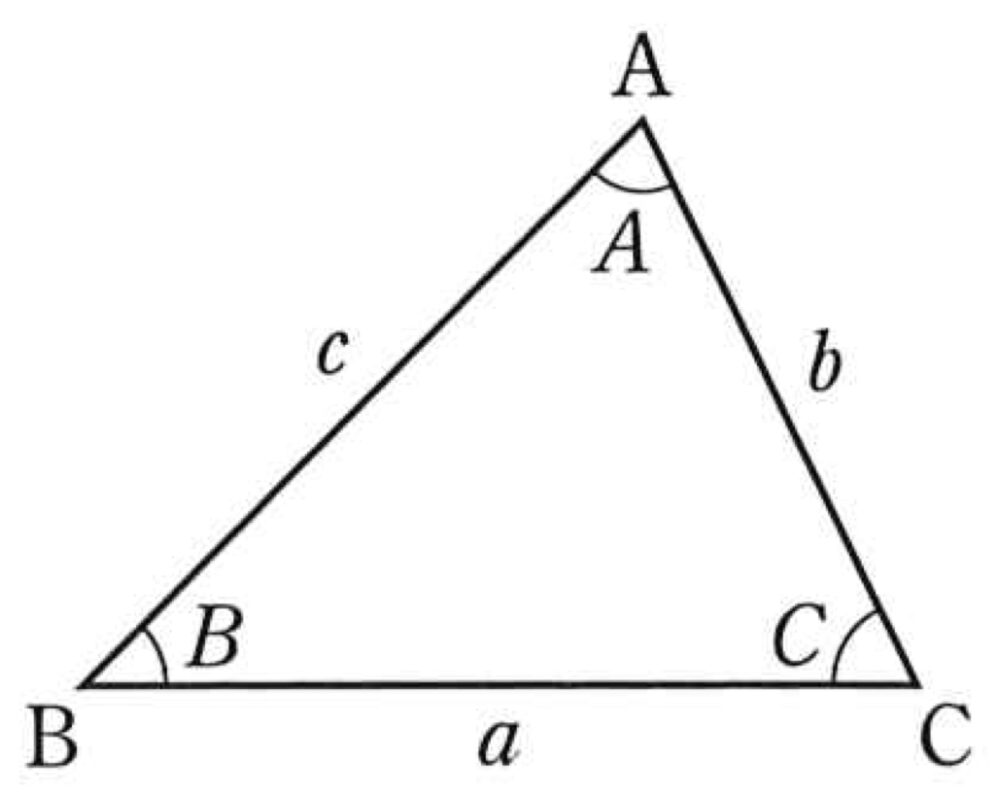
三角形 \(ABC\) において、辺 \(AB\) の長さを \(c\)、辺 \(CA\) の長さを \(b\) で表す.
\(\angle{ACB}=3\angle{ABC}\) であるとき、\(c<3b\) を示せ.
正弦定理

☆正弦定理を使うタイミング☆
- \(1\) つの辺と向かい合う角に関して情報が \(2\) セット
- 外接円の半径についての情報
が与えられたら正弦定理!
※余弦定理は様々な場面で利用できます。細かく言い出せばキリがないのですが、基本的に正弦定理が無理だったら余弦定理というぐらいの使い分けでOK!
3倍角の公式の利用
\(\sin3\theta=3\sin\theta-4\sin^3\theta\)
\(\cos3\theta=4\cos^3\theta-3\cos\theta\)
\(\theta=\angle{ABC}\) とおくと、\(\angle{ACB}=3\theta\)
正弦定理から、\(\sin3\theta\) が表れるので、3倍角の公式を利用する.
※三角関数の加法定理、2倍角、半角、3倍角、和積の公式など、1つでも不安があるものがあれば
【三角関数】公式まとめ&差がつく入試問題演習 を確認しましょう!
解答
\(\theta=\angle{ABC}\) とおくと、\(\angle{ACB}=3\theta\) .
三角形の内角の和は \(\pi\) であるから、\(\angle{BAC}=\pi-4\theta\)
よって、\(\theta>0\) かつ \(\pi-4\theta>0\) より
\(0<\theta<\displaystyle\frac{\pi}{4}\)

この結果を利用するかどうかはさておき、
自分で設定した文字については常に範囲を調べる習慣を!
このとき正弦定理より、
\(\displaystyle\frac{b}{\sin\theta}=\displaystyle\frac{c}{\sin 3\theta}\)
\(c=\displaystyle\frac{\sin 3\theta}{\sin\theta}b\)
ここで、3倍角の公式 \(\sin 3\theta=3\sin\theta-4\sin^3\theta\) より、
\(c=(3-4\sin^2\theta)b\)
よって、\(3b-c=4b\sin^2\theta>0\)
したがって、\(c<3b\) が成立する.







コメント