【2023東北大学・理系・第４問】複素数平面(αの5乗根の利用)

解答・解説

(１)　\(x^4+x^3+x^2+x+1\) は \(f(x)\) で割り切れることを示せ．

\(a=\displaystyle\frac{\sqrt{5}-1}{2}\) より

\(a+\displaystyle\frac{1}{2}=\displaystyle\frac{\sqrt{5}}{2}\)

両辺を \(2\) 乗すると

\(\left(a+\displaystyle\frac{1}{2}\right)^2=\left(\displaystyle\frac{\sqrt{5}}{2}\right)^2\)

\(a^2+a-1=0\) ・・・①

\(x^4+x^3+x^2+x+1\) を \(x^2-ax+1\) で割ると

\(x^4+x^3+x^2+x+1\\=(x^2-ax+1)\left\{x^2+(a+1)x+a^2+a\right\}+(a^3+a^2-a)x-a^2-a+1\) より

余りは \((a^3+a^2-a)x-a^2-a+1\)

ここで①の結果を利用すると

\((a^3+a^2-a)x-a^2-a+1=a(a^2+a-1)x-(a^2+a-1)=0\)

となり，整式 \(x^4+x^3+x^2+x+1\) は \(f(x)\) で割り切れる．

(２)　\(\alpha\) を極形式で表せ．

(１)の結果から

\(x^4+x^3+x^2+x+1=f(x)\left\{x^2+(a+1)x+a^2+a\right\}\)

この両辺に \(x-1\) をかけると

\((x-1)(x^4+x^3+x^2+x+1)=(x-1)f(x)\left\{x^2+(a+1)x+a^2+a\right\}\)

\(x^5-1=(x-1)f(x)\left\{x^2+(a+1)x+a^2+a\right\}\)

したがって，\(x^5-1=0\) の解のうち，\(1\) でないものは

\(f(x)\left\{x^2+(a+1)x+a^2+a\right\}=0\) の解となる．

\(x^5-1=0\) の解は，\(|x^5|=|x|^5=1\) より \(|x|=1\) なので

\(x=\cos\theta+i\sin \theta\) とおける．

ド・モアブルの定理から

\(x^5=\cos 5\theta+i\sin 5\theta\)

よって，\(x^5-1=0\)

\(\iff\) \(\cos 5\theta+i\sin 5\theta=1\)

\(\iff\) \(5\theta=2\pi k\) ( \(k\) は整数 )

\(\iff\) \(\theta=\displaystyle\frac{2\pi k}{5}\)

ゆえに \(f(x)\left\{x^2+(a+1)x+a^2+a\right\}=0\)

\(\iff\) \(x=\cos \displaystyle\frac{2\pi k}{5}+i\sin\displaystyle\frac{2\pi k}{5}\) ( \(k=1,2,3,4\) )

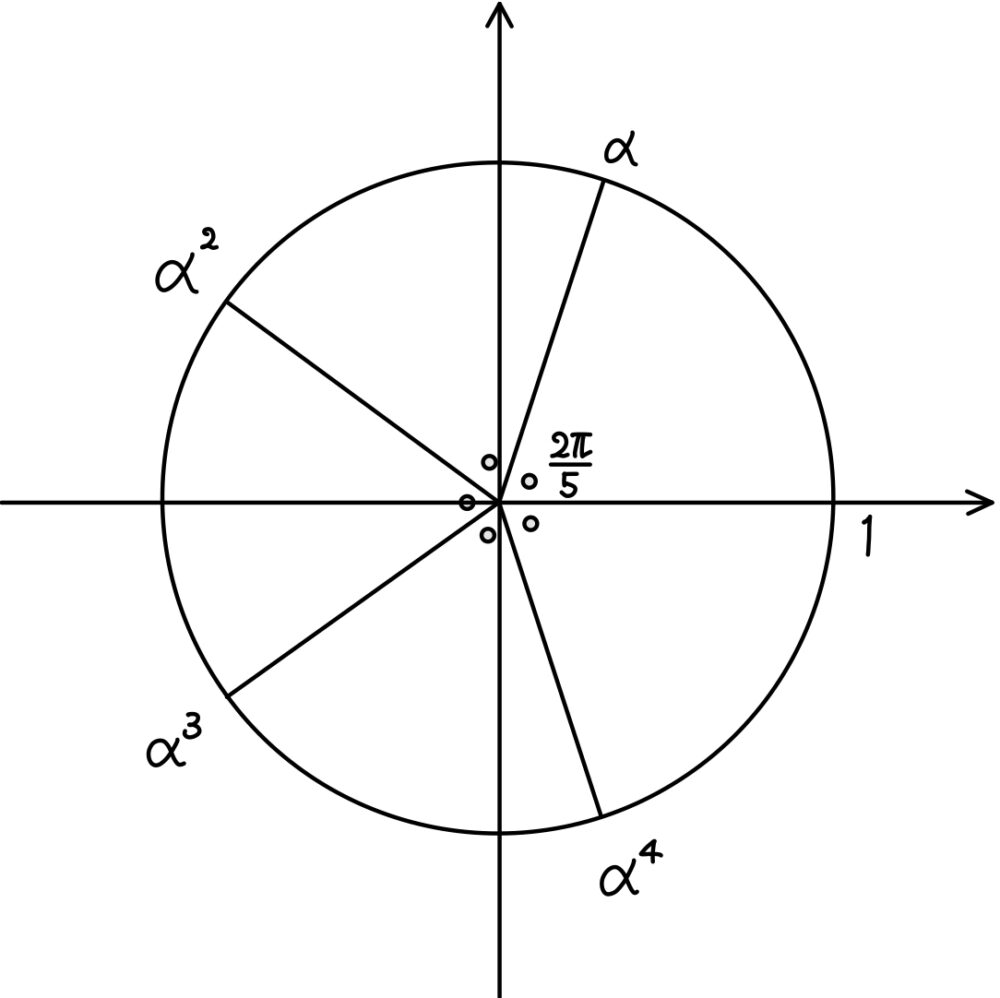\(f(x)=0\)  \(\iff\) \(x^2-ax+1=0\) の解は

実部が \(\displaystyle\frac{a}{2}=\displaystyle\frac{\sqrt{5}-1}{4}>0\)

となるので，\(x=\alpha,\alpha^4\)

このうち虚部が正であるものは \(\alpha\) より

\(\alpha=\cos\displaystyle\frac{2\pi}{5}+i\sin\displaystyle\frac{2\pi}{5}\)

(３)　\(\alpha^{2023}+\alpha^{-2023}\) の値を求めよ．

\(\alpha^5=1\) より

\(\alpha^{2023}+\alpha^{-2023}=\left(\alpha^5\right)^{404}\cdot\alpha^3+\left(\alpha^5\right)^{-405}\cdot\alpha^2=\alpha^3+\alpha^2\)

(２)の図より，\(f(x)=0\) の解が \(\alpha,\alpha^4\) で

\(x^2+(a+1)x+1=0\) の解が \(\alpha^2,\alpha^3\) となるので，

解と係数の関係から

\(\alpha^3+\alpha^2=-(a+1)=-\displaystyle\frac{1+\sqrt{5}}{2}\)