放物線の定義｜焦点(0,0)，準線y=-2の放物線(2021浜松医科大学・医学部)

【2021浜松医科大学・医学部・第２問(２)】

焦点が \((0,0)\) ，準線 \(y=-2\) の放物線と直線 \(y=2\) の交点を \(P\) とする．

( a )　\(P\) の座標を求めよ．

( b )　( a ) とは別の解法で \(P\) の座標を求めよ．

放物線の定義

放物線の定義

平面上で，定点 \(F\) と，\(F\) を通らない定直線 \(L\) からの距離が等しい点 \(P\) の軌跡を放物線という．

点 \(F\) をその焦点，直線 \(L\) を準線という．

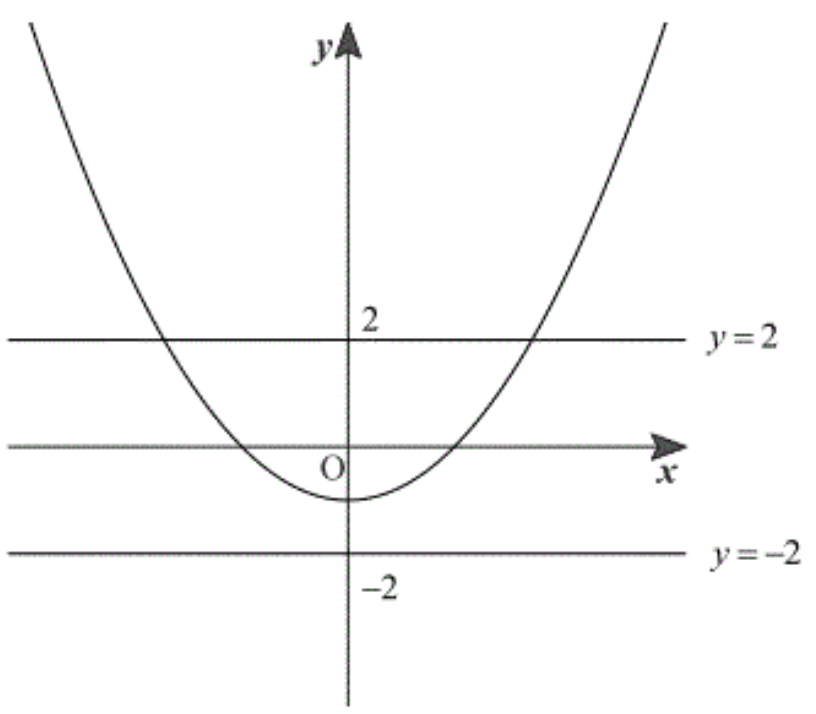原点を \(O\) ，点 \(P(t,2)\) とする．

放物線の定義から，\(OP\) の距離と点 \(P\) と直線 \(y=-2\) の距離が等しいので

\(OP=2-(-2)=4\)

\(\iff\) \(\sqrt{t^2+4}=4\)

よって，\(t=\pm 2\sqrt{3}\)

したがって，\(P(\pm 2\sqrt{3},2)\)

放物線上の点を \((X,Y)) とおく．

焦点が \((0,0)\) ，準線 \(y=-2\) の放物線より

\(\sqrt{X^2+Y^2}=|Y-(-2)|\)

よって，\(X^2+Y^2=Y^2+4Y+4\) より \(Y=\displaystyle\frac{1}{4}X^2-1\)

ゆえに，題意を満たす放物線は \(y=\displaystyle\frac{1}{4}x^2-1\)

これと \(y=2\) の交点は

\(2=\displaystyle\frac{1}{4}x^2-1\)

\(\iff\) \(x=\pm 2\sqrt{3}\)

したがって，\(P(\pm 2\sqrt{3},2)\)