正の実数 \(x , y , z\) において
\(x^3+y^3+z^3≧3xyz\) を示せ.
不等式の証明の解き方(まとめ)
【1】差をとる
【2】グラフの利用
【3】最小値をとらえる
【4】有名不等式の利用
【5】その他(凸関数の利用など)
【1】差をとって正(または負)になることを示す
(ア) 2 乗(平方完成)の形を作る
👉 \(a^2≧0\) を利用
(イ) 因数分解
👉 「正×正」や「負×負」の形を作る
※差をとっただけでは処理できないとき
両辺が正であれば、2 乗の差をとって考える
【2】グラフの利用
※不等式は、両辺のグラフの上下関係を表している.
グラフを描くことで視覚的にとらえる.
【3】最小値をとらえる
ある範囲において \(f(x)≧0\)
☞ (ある範囲における \(f(x)\) の最小値) \(≧0\)
より詳しく確認したい場合は、
を参考にご確認ください!
【4】有名不等式の利用
(ア) 相加平均・相乗平均の関係
(イ) コーシー・シュワルツの不等式
(ウ) 三角不等式 など
【5】その他(凸関数の利用など)
発展的な考え方です。
にまとめています。
【解法 Ⅰ 】差をとる
(左辺)-(右辺)
\(=x^3+y^3+z^3-3xyz\)
\(=(x+y+z)(x^2+y^2+z^2-xy-yz-zx) \)
\(x , y , z\) は正の実数より
\(x+y+z>0\)
よって、\( x^2+y^2+z^2-xy-yz-zx ≧ 0\) を示せばよい.
[解法 Ⅰ -①] 文字固定& 2 乗(平方完成)の形へ
\(x\) の関数として見る(\(y , z \) は固定して、定数扱いで考える)
\(x\) について降べきの順に並べると、
\(x^2-(y+z)x+y^2-yz+z^2\)
\(=(x-\displaystyle\frac{y+z}{2})^2-(\displaystyle\frac{y+z}{2})^2 +y^2-yz+z^2\)
\(=(x-\displaystyle\frac{y+z}{2})^2+\displaystyle\frac{3}{4}(y^2-2yz+z^2)\)
\(=(x-\displaystyle\frac{y+z}{2})^2+\displaystyle\frac{3}{4}(y-z)^2≧0\)
等号成立は、
\(x=\displaystyle\frac{y+z}{2}\) かつ \(y=z\)
つまり、\(x=y=z\) のとき
[解法 Ⅰ -②]相加平均・相乗平均の関係の利用
相加平均・相乗平均の関係
\(a≧0 , b≧0\) のとき
\(a+b≧2\sqrt{ab}\) が成立
等号成立は \(a=b\) のとき
相加平均・相乗平均の関係より
\(x^2+y^2≧\sqrt{x^2y^2}=2xy\)
\(y^2+z^2≧\sqrt{y^2z^2}=2yz\)
\(z^2+x^2≧\sqrt{z^2x^2}=2zx\)
各辺を加えて 2 で割ると
\( x^2+y^2+z^2 ≧ xy+yz+zx\)
\( x^2+y^2+z^2-xy-yz-zx ≧ 0\)
等号成立は、
\(x=y\) かつ \(y=z\) かつ \(z=x\)
つまり、\(x=y=z\) のとき
[解法 Ⅰ -③]コーシー・シュワルツの不等式の利用
コーシー・シュワルツの不等式
・\((a^2+b^2)(x^2+y^2)≧(ax+by)^2\)
等号成立は、\(a : b = x : y\) のとき
・\((a^2+b^2+c^2)(x^2+y^2+z^2)≧(ax+by+cz)^2\)
等号成立は、\(a : b : c = x : y : z\) のとき
コーシー・シュワルツの不等式
\((a^2+b^2+c^2)(x^2+y^2+z^2)≧(ax+by+cz)^2\)
に \(a=y , b=z , c=x\) を代入すると
\((y^2+z^2+x^2)(x^2+y^2+z^2) ≧ (yx+zy+xz)^2\)
\((x^2+y^2+z^2)^2 ≧ (xy+yz+zx)^2\)
\(x , y , z\) は正の実数より
\(x^2+y^2+z^2 ≧ xy+yz+zx\)
等号成立は、\(y : z : x =x : y : z\)
よって \(x=y=z\) のとき
[解法 Ⅰ -④]有名な解法
この解法は知らないと思いつきません.
教科書にも載っているような超有名解法です.
\( x^2+y^2+z^2-xy-yz-zx\)
\(=\displaystyle\frac{1}{2}(2x^2+2y^2+2z^2-2xy-2yz-2zx)\)
\(=\displaystyle\frac{1}{2}\left\{(x^2-2xy+y^2)+(y^2-2yz+z^2)+(z^2-2zx+x^2)\right\}\)
\(=\displaystyle\frac{1}{2}\left\{(x-y)^2+(y-z)^2+(z-x)^2\right\}≧0\)
\(x=y\) かつ \(y=z\) かつ \(z=x\)
つまり、\(x=y=z\) のとき
【解法Ⅱ】最小値をとらえる
ある範囲において \(f(x)≧0\)
☞ (ある範囲における \(f(x)\) の最小値) \(≧0\)
\(f(x)=x^3-3yzx+y^3+z^3\) とおく.
本問は、
「\(x>0\) において、\(f(x)≧0\) を示せ」
という問題と言い換えることができる.
\(f^{\prime}(x)=3x^2-3yz=3(x^2-yz)\)
\(f^{\prime}(x)=0\) を考えると
\(x=±\sqrt{yz}\)
\(x>0\) における増減表は以下の通りであり、
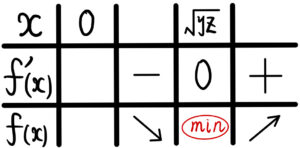
\(f(\sqrt{yz})\)
\(=\sqrt{yz})^3-3yz\sqrt{yz}+y^3+z^3\)
\(=y^3-2yz\sqrt{yz}+z^3\)
\(=(y\sqrt{y}- z\sqrt{z})^2≧0\)
したがって、\(x>0\) において \(f(x)≧0\)
等号成立は、\(x=\sqrt{yz}\) かつ \( y\sqrt{y}=z\sqrt{z}\)
つまり、\(x=y=z\) のとき
【参考】相加平均・相乗平均の関係(3つ)の証明
今、様々な不等式の証明の方法を用いて証明を与えてきた結果、
\(x^3+y^3+z^3≧3xyz\) が分かったが、この式において、
\(x= \sqrt[3]{a} , y= \sqrt[3]{b} , z= \sqrt[3]{c}\) とおくと
\(a+b+c≧3\sqrt[3]{abc}\)
( 3 つの相加平均・相乗平均の関係が証明できた)
等号成立は、\(x=y=z\) より
\(\sqrt[3]{a} = \sqrt[3]{b} = \sqrt[3]{c}\)
つまり\(a=b=c\) のとき









コメント