【2023東京大学・文科・第４問】空間図形(半径１の球面上の四面体ABCDの体積)

解答・解説

(１)　三角形 \(ABC\) の面積

\(AC=BC=x\) とおく

\(\triangle ABC\) で余弦定理より

\(1^2=x^2+x^2-2\cdot x\cdot x\cdot\displaystyle\frac{4}{5}\)

\(x^2=\displaystyle\frac{5}{2}\)

\(x>0\) より \(x=\displaystyle\frac{\sqrt{10}}{2}\)

また，\(\cos\angle ACB=\displaystyle\frac{4}{5}\) より

\(\sin \angle ACB=\sqrt{1-\left(\displaystyle\frac{4}{5}\right)^2}=\displaystyle\frac{3}{5}\)

したがって，

\(\triangle ABC=\displaystyle\frac{1}{2}\cdot x \cdot x \cdot\displaystyle\frac{3}{5}=\displaystyle\frac{3}{10}x^2=\displaystyle\frac{3}{4}\)

(２)　四面体 \(ABCD\) の体積

\(4\) 点 \(A\) , \(B\) , \(C\) ，\(D\) を通る半径 \(1\) の球の中心を \(O\)，

\(AB\) の中心を \(M\)，\(CD\) の中心を \(N\) とおく．

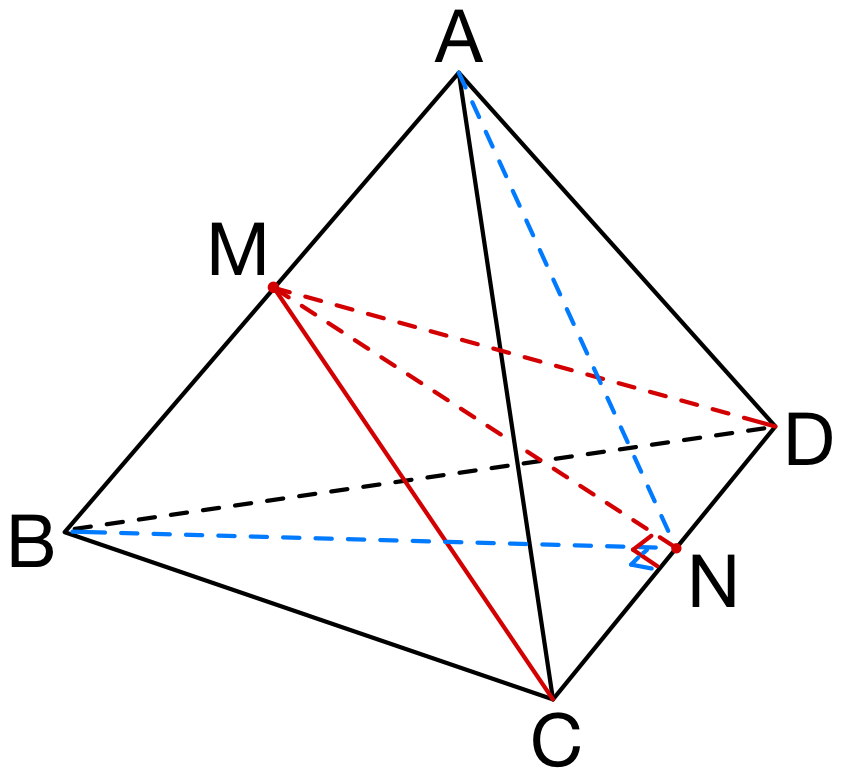\(AC=BC\)，\(AD=BD\)，\(\angle ACB=\angle ADB\) より

\(\triangle ABC≡\triangle ABD\) となるから
点 \(C\) , \(D\) は平面 \(ABN\) に関して対称かつ

点 \(A\) , \(B\) は平面 \(MCD\) に関して対称である．

ゆえに，点 \(O\) は線分 \(MN\) 上にある．

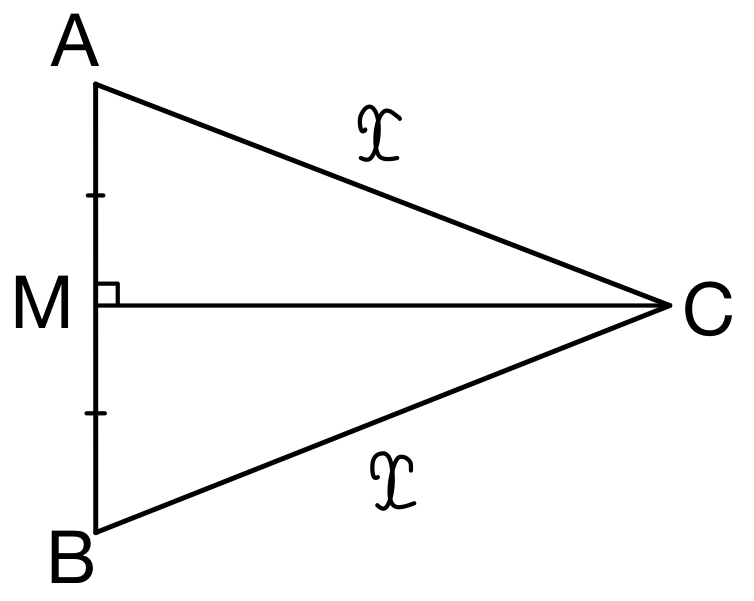ここで，直角三角形 \(AMC\) に注目すると

\(AM^2+CM^2=AC^2\)

\(\left(\displaystyle\frac{1}{2}\right)^2+CM^2=x^2=\displaystyle\frac{5}{2}\)

\(CM^2=\displaystyle\frac{9}{4}\)

\(CM>0\) より \(CM=\displaystyle\frac{3}{2}\)

また，\(\triangle OAB\) は一辺の長さが \(1\) の正三角形であるから，\(OM=\displaystyle\frac{\sqrt{3}}{2}\)

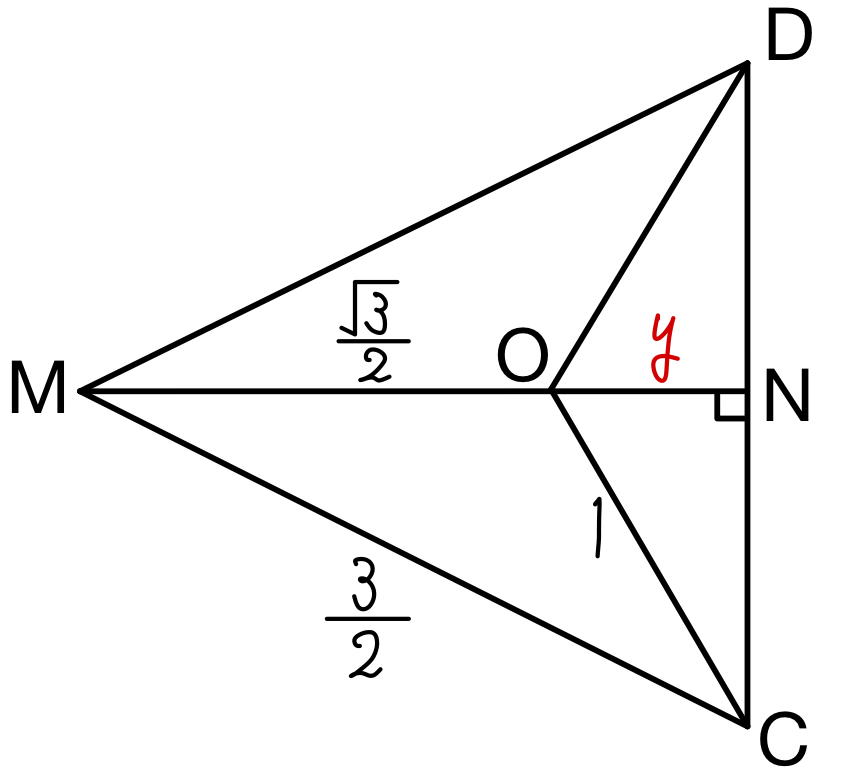\(ON=y\) とおくと

\(\triangle CMN\) に注目すると

\(CM^2=MN^2+CN^2=MN^2+(OC^2-ON^2)\)

\(\left(\displaystyle\frac{3}{2}\right)^2=\left(\displaystyle\frac{\sqrt{3}}{2}+y\right)^2+(1^2-y^2)\)

\(y=\displaystyle\frac{\sqrt{3}}{6}\)

したがって求める体積 \(V\) は

\(V=\displaystyle\frac{1}{3}\cdot \triangle ABN\cdot CD\) で

\(\triangle ABN=\displaystyle\frac{1}{2}AB\cdot MN=\displaystyle\frac{1}{2}\cdot 1\cdot \displaystyle\frac{2\sqrt{3}}{3}=\displaystyle\frac{\sqrt{3}}{3}\)

\(CD=2CN=2\sqrt{1^2-y^2}=\displaystyle\frac{\sqrt{33}}{3}\)

以上から，\(V=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{\sqrt{3}}{3}\cdot\displaystyle\frac{\sqrt{33}}{3}=\displaystyle\frac{\sqrt{11}}{9}\)