2変数関数の最大値・最小値の求め方（予選決勝法）１文字固定

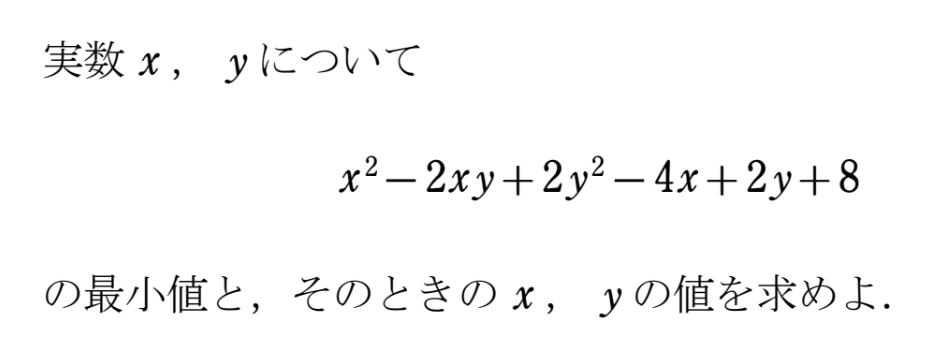
考え方

２変数関数は、やや発展的な内容ではありますが、超有名な頻出テーマになりますので、考え方をしっかり理解しておきましょう！

２変数関数のMax・min

👉１文字固定（予選決勝法）

そもそも２変数関数は、２文字あるから大変！

だから１文字ずつ考えようっていうやり方です。

甲子園をイメージしてください。

全国の高校が甲子園で試合をし、日本一を決めようとしたらすごく大変ですよね？

だからまず最初にそれぞれの都道府県ごとに予選を行い、そこで１位になったチームが次に甲子園で決勝大会を行うわけです。

２変数関数も基本的には同じことをします。

ちなみに甲子園の例では、「最大値の中の最大値」を求める作業です。

本問では、「最小値の中の最小値」を求める作業を行っていきます。

まず最初に、 $x$ だけに注目しましょう！（ $y$ を固定・・・$y$ は数字の２や３だと思ってください）

そうすると今回の問題は、$x$ の２次関数になります。

そこで、$x$ について降べきの順に並べると

$$x^2-2(y+2)x+2y^2+2y+8$$

あとは $x$ の２次関数と考えて最小値を求めます。（平方完成します）

$x^2-2(y+2)x+2y^2+2y+8\\=\left\{x^2-\left(y+2\right)\right\}^2-(y+2)^2+2y^2+2y+8\\=\left\{x^2-\left(y+2\right)\right\}^2+y^2-2y+4$

$x=y+2$　のとき　最小値は　$y^2-2y+4$

これで予選終了！

最後に、最小値の中の最小値を調べる（決勝をする）

$y^2-2y+4=(y-1)^2+3$

となり、最小値の中の最小値は　３　（$x＝3、y＝1$のとき）と求まります。

・２変数関数の最大・最小問題に出会ったら、予選（１文字固定）をしてから決勝大会を行う！

※高校数学で最も大切な分野は、数学Ⅰで学習する「２次関数」です。２次関数の問題の中ではやや発展的な内容にはなりますが、超有名な頻出テーマですので、解法の流れをしっかりと理解して身につけましょう！

２変数関数についての類題です。演習にどうぞ！

リンク