学校の授業ではあまり扱わないが、入試では頻出テーマ
整数問題 【2021昭和大学・医】√(n^2-9n+19)^(n^2+5n-14)=1を満たす自然数n
aのb乗が1となるa,bの条件。a=1のとき、b=0のとき、a=-1かつbが4の倍数の3つのタイプ。差がつく良問。2021昭和大学・医学部・第２問(２)。整数
2022年入試問題 【2022上智大学・理工】cos61°の近似値｜近似式について
導関数の定義から、|h|が十分に小さいときf(x)の近似値、近似式を考える。cos61°の近似値について。数学Ⅲ：微分の応用、速度と近似式。早慶、GMARCH、関関同立大学対策。
積分まとめ 【2021京都大学・理系・第4問】曲線の長さ(数学Ⅲ：積分の応用)
曲線の長さの公式と例題。基本的な公式に当てはめて計算するだけの基礎問題。1/cosxの置換積分の計算も典型・頻出。2021京大(理系)過去問演習・対策。
数列 【2010京都大学】数学的帰納法(全段仮定)｜差がつく良問(数学B数列)
n≦kを満たすすべてのnで成り立つと仮定し，n=k+1のときに示す．数学的帰納法の有名３タイプのうちの「全段仮定法」．経験で差がつく入試問題．2010京大過去問演習・対策。数学B。また別解として背理法の紹介。
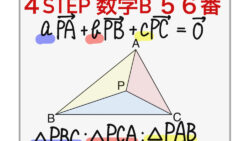
共通テスト(センター試験) 【頻出！公式】aPA+bPB+cPC=0(ベクトル)の点Pの位置と三角形の面積比
aPA+bPB+cPC=0(ベクトル)とき、点Pの位置について。また△PBC:△PCA:△PAB(三角形の面積比)
頻出！共通テスト・私立大学入試のための裏技公式！数学B：４STEP56番(平面ベクトル)
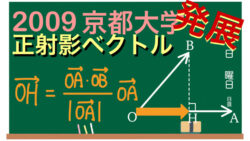
ベクトル 【2009京都大学】正射影ベクトルとは？正射影ベクトルの利用・演習
差をつける解法。正射影ベクトルについての公式・考え方(使い方)・求め方・解法を紹介。京大過去問演習。２次試験対策。数学Bベクトル。発展
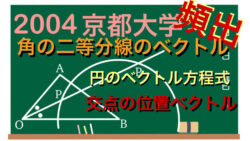
ベクトル 【2004京都大学(文)】角の二等分線と円のベクトル方程式の交点の位置ベクトル
ポイントは角の２等分線上のベクトルについて。また中心がB、半径ルート10の円のベクトル方程式との交点。数学B：平面ベクトル。京大過去問演習。２次試験対策。差がつく良問。
ベクトル 【2022九州大学】平面に対称な点｜外積・平面の方程式・点と面の距離の公式｜差がつく良問
学校では学習しないが入試頻出の差がつくテーマ。数学B空間ベクトル。２次試験対策。平面の方程式と平面に関して対称な点。頻出・重要問題。外積、平面の方程式、点と面の距離の公式の利用。
ベクトル 【2006神戸大学・文】角の二等分線のベクトル｜差がつく良問
数学B平面ベクトル。内角の二等分線のベクトルの公式・証明・利用。差がつく有名問題。
４STEP発展問題にものっている問題。２次試験数学対策。
ベクトル 平面の方程式・正領域と負領域【1993神戸大学・理(後期)】
学校では習わない、差がつく入試問題。数学Bの平面の方程式、数学Ⅱ図形と方程式の正領域・負領域における入試問題演習。新大過去問・２次試験対策。発展
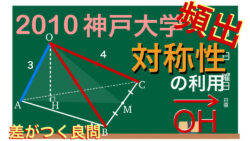
ベクトル 【対称性の利用】空間ベクトル(共面条件・ 垂直条件)｜2010神戸大学
与えられた条件から図形の対称性に気づき，文字数を減らす。ちょっとした意識で差がつく重要ポイント！
また頻出の共面条件(係数の和が１)や垂直条件(平面とベクトルが垂直)を利用した良問。神戸大過去問演習。２次試験対策。数学B空間ベクトル。
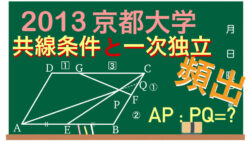
ベクトル 【2013京都大学】１次独立と共線条件・幾何(相似)を利用した別解
平面図形の問題を見たら幾何、ベクトル、座標の３パターンの解法を考える癖を！平行四辺形におけるAP:PQ。点P、Qをそれぞれ２通りずつで表し、APベクトル、AQベクトルを求める．受験数学における頻出・重要問題。数学Bベクトル。また幾何(相似)を利用した別解を紹介。
整数問題 【無限下降法】a^3+2b^3+4c^3=2abcを満たす整数はa=b=c=0のみを示せ｜お茶の水女子大
背理法の一種である無限下降法の演習問題。有名問題であるが学校では学習しない差がつく頻出・良問。1985年お茶の水女子大学過去問。２次試験対策。数学A：整数問題
整数問題 【頻出】f(k-1),f(k),f(k+1)が整数のとき,正の整数nでf(n)は整数
整数と関数の頻出総合問題。連立方程式から整数であることの証明、数学的帰納法を用いてf(n)が整数であることの証明。
２次試験対策。大学受験数学。過去問演習。
複素数と方程式 【2004京都大・文(後期)】f(x+y)=f(x)f(y),f(3)=8のときf(1)の値
解析的分野の論証問題。差がつく良問。2004京都大学・文系・後期試験過去問解説。
式と証明 相加・相乗・調和平均の関係・証明【2008奈良女子大学】
相加平均・相乗平均・調和平均(逆数の平均の逆数)の大小関係の証明と利用。頻出・重要不等式。
整数問題 2022神戸大学・文・第３問【整数・対数】a^m=b^n=(ab)^5 のとき、aとbの関係式
【頻出問題】(１)常用対数を用いた有名証明問題(教科書レベル)。(２)整数問題・積の形に変形の典型問題。
(３)(１)、(２)の誘導から答えを導く。数学Ａ整数問題、数学Ⅱ指数・対数関数。
2次関数 【2次関数・有名問題】すべて・ある実数に対してf(x)>g(x)の成立条件
２次関数の有名問題。２つの２次関数のグラフの上下関係(不等式)を満たす条件。
最大値、最小値の関係に注目。定期考査・２次試験対策。数学Ⅰ
式と証明 【頻出】有理数の解をもつ⇒その解は整数｜2001神戸大学・理
有理数、整数解に関する有名頻出問題。互いに素、背理法を用いて証明。
数学Ａ整数問題２次試験対策。神戸大学過去問
場合の数・確率 【確率漸化式】2020大阪大学・文系[第２問] 解き方・考え方｜入試問題演習
学校の授業ではあまり扱われないが、数学の２次試験では頻出重要テーマの確率漸化式について、考え方、立式の仕方について解説。
数学Ａの確率、数学Ｂの数列(漸化式)の融合総合問題。２次試験対策に！
数列 医学部(難関理系)攻略｜三角関数・数学的帰納法(２段仮定)考え方【滋賀医科大学】
三角比の定義、３倍角、和積の公式、減少関数、偶関数など、三角関数のポイントが多く詰まった良問。
また、背理法、２段仮定の数学的帰納法と、方針・考え方を学ぶことができる１問。
複素数と方程式 ３つの相加・相乗平均の関係｜実践問題【慶応義塾大学】
相加平均・相乗平均の関係は入試頻出テーマ。
ただ公式を覚えているだけでは使えません。しっかりと使うタイミングを練習するための良問。
ベクトル 平面図形｜解法研究・思考力を鍛える【1994 名古屋大学】
平面図形の問題は、幾何・座標・ベクトルの３つを考える習慣を身につけることが大切。
分野を決めつけず、３タイプを考える癖をつけるための演習問題
整数問題 【整数問題(素数)】n^k+kが素数｜実験することの大切さ｜2021 東京学芸大学
整数問題の極意は、「実験」から規則・法則を見出し、方針を見つけていくこと！
しっかりと手を動かし、実験を行う練習として良問です。