

数学Bの教科書(発展)には書かれていますが、おそらくほとんどの学校では扱わないテーマです、
しかし、難関大学では頻出テーマでもあり、知っているかどうかで差がつく分野になります。
ここでは「平面の方程式」「直線の方程式」「点と平面の距離の公式」についての説明、そして簡単な例題を用いて使い方を学習しましょう。![]()
平面の方程式(公式・証明)
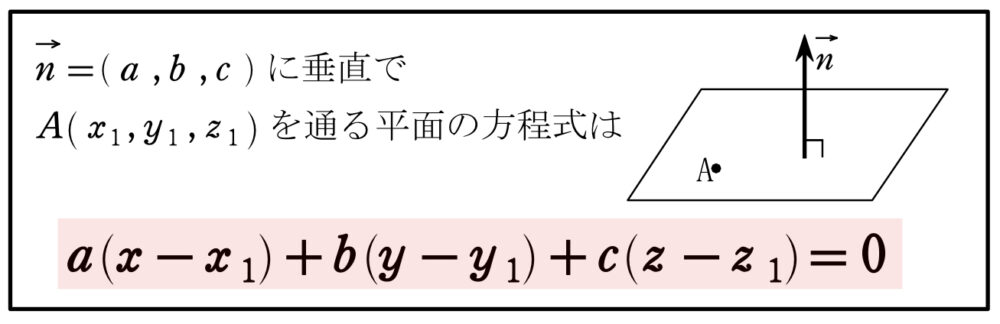
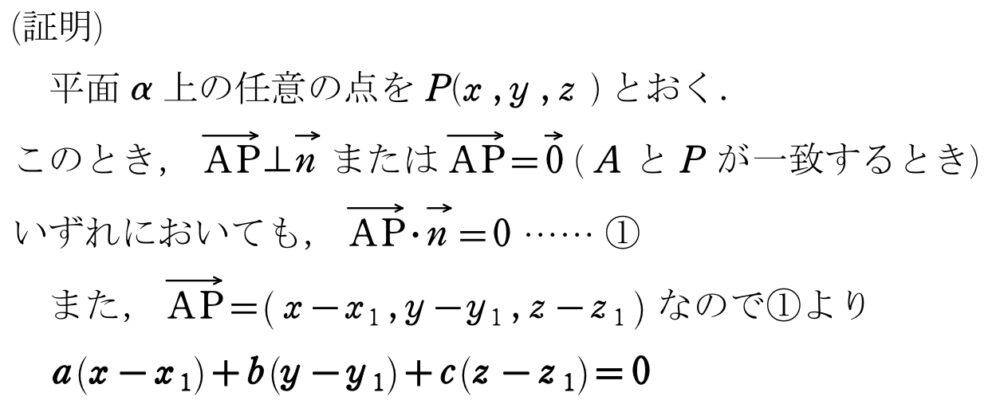
平面の方程式(法線ベクトル)

参考(\(x\)切片,\(y\)切片,\(z\)切片を通る平面の方程式)

\(x\),\(y\),\(z\) の1次式方程式
👉 平面の方程式
平面の方程式(練習問題)

平面の方程式を求めるためには、
① 法線ベクトル
② 通る点
の2つの情報が分かればば良い!
【解答】平面の方程式(練習問題)

《参考》外積の利用
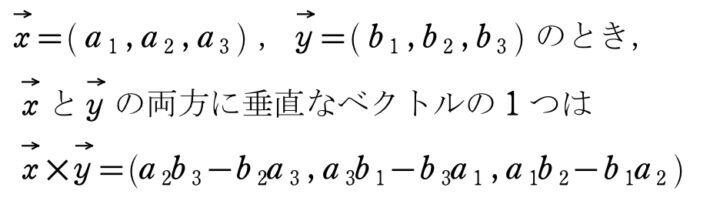
※ \(\vec{x}\times\vec{y}\) を \(\vec{x}\) と \(\vec{y}\) の外積という
※ 外積は高校数学では学習しません。(教科書に載っていません)そのため,記述式の答案で使用すると、減点される可能性があります。使用する場合は、記述として解答に残さないこと!
直線の方程式

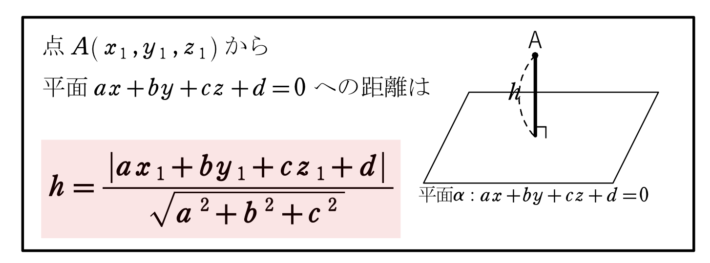
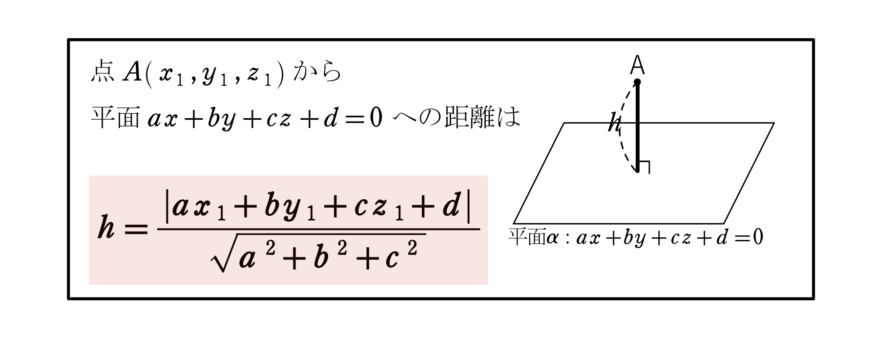
点と平面の距離の公式・証明

練習問題

(1)平面の方程式の公式利用
(2)の前半:点と面の距離の公式利用
(2)の後半:直線の方程式(媒介変数表示)の利用
(3)三角形の面積公式利用
【超重要公式】三角形の面積公式
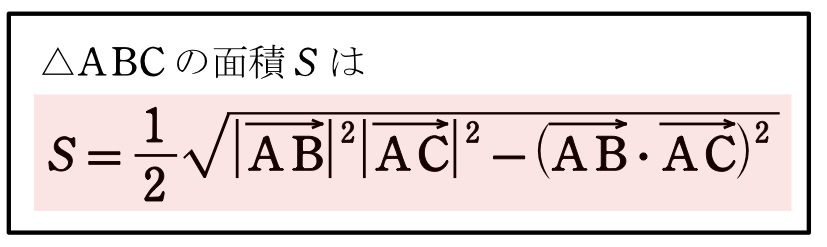
この公式は、最重要公式の1つです!
解答

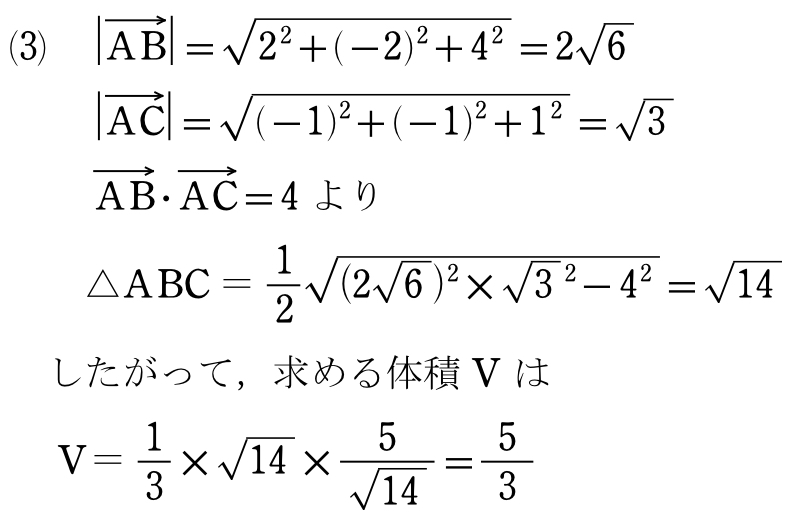
空間の方程式は様々な空間の問題で応用ができます。
また大学によっては頻出テーマでもあります。
授業ではなかなか扱わないからこそ、このようなところで経験値を積んでおきましょう!
下記に類題、また平面の方程式などを利用する総合問題を抜粋しています。演習としてご利用ください!
類題演習
【2021 宮崎大学・改】
\(p\)、\(q\) を正の実数とする.点 \(O\) を原点とする座標空間において、\(4\) 点
\(A ( 1 , 1 , 0 )\)、\(B ( 0 , 2 , 0 )\)、\(C ( 0 , 0 , 6 )\)、\(D ( p , q , 1 )\)
をとる.\(3\) 点 \(A\)、\(B\)、\(C\) を含む平面を \(\alpha\) 、\(\triangle{OAD}\) の面積を \(S\) とする.
点 \(D\) が平面上 \(\alpha\) を動くとき、面積 \(S\) の最小値を求めよ.
解答・考え方は⏬

その他、平面の方程式・点と面の距離の公式・外積などを利用した入試問題









コメント