【2021数学ⅡB(第1日程)】第１問[１](三角関数)

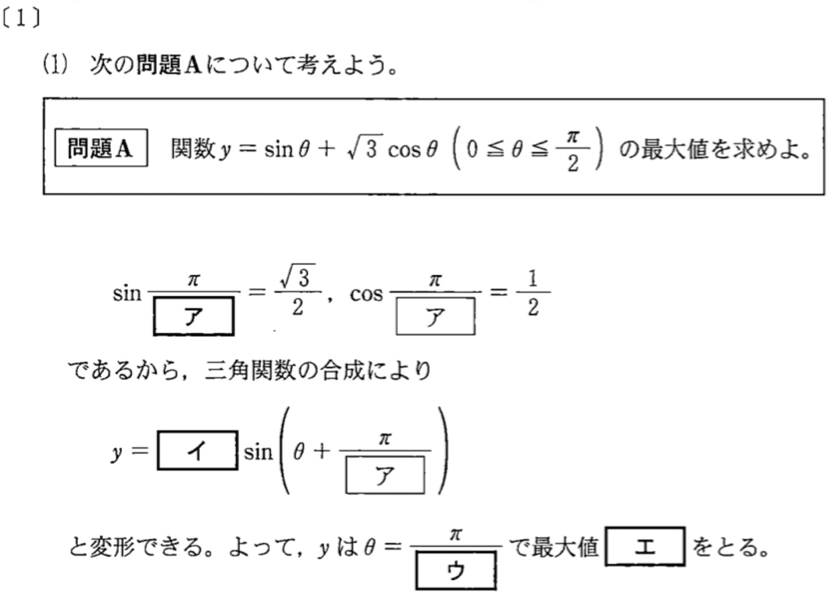
(１)問題と解答・解説《ア〜エ》

解答・解説《ア〜エ》

$0≦\theta≦\displaystyle\frac{\pi}{2}$ において

$\sin \displaystyle\frac{\pi}{3}=\displaystyle\frac{\sqrt{3}}{2}$ , $\cos \displaystyle\frac{\pi}{3}=\displaystyle\frac{1}{2}$ ・・・《ア》

であるから，三角関数の合成により

$y=2\left(\sin \theta\cdot\displaystyle\frac{1}{2}+\cos \theta\cdot\displaystyle\frac{\sqrt{3}}{2}\right)$

$=2\left(\sin\theta\cos\displaystyle\frac{\pi}{3}+\cos \theta\sin\displaystyle\frac{\pi}{3}\right)$

$=2\sin\left(\theta+\displaystyle\frac{\pi}{3}\right)$ ・・・《イ》

よって，$0≦\theta≦\displaystyle\frac{\pi}{2}$ のとき

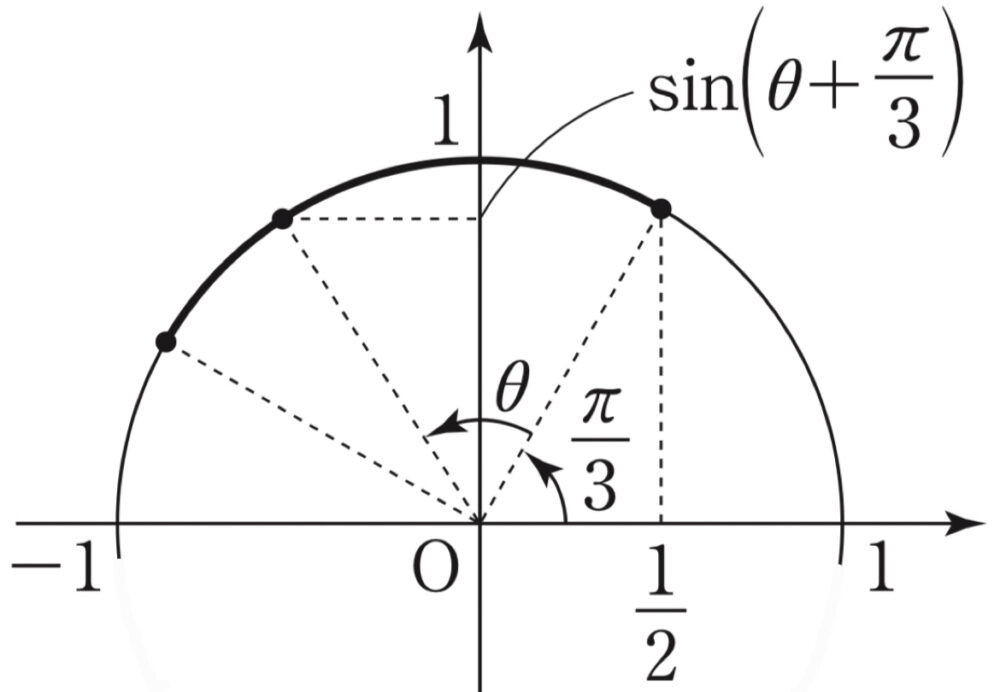$\displaystyle\frac{\pi}{3}≦\theta+\displaystyle\frac{\pi}{3}≦\displaystyle\frac{5\pi}{6}$ なので

$y$ は $\theta+\displaystyle\frac{\pi}{3}=\displaystyle\frac{\pi}{2}$

つまり $\theta=\displaystyle\frac{\pi}{6}$ で最大値： $2$ ・・・《ウエ》

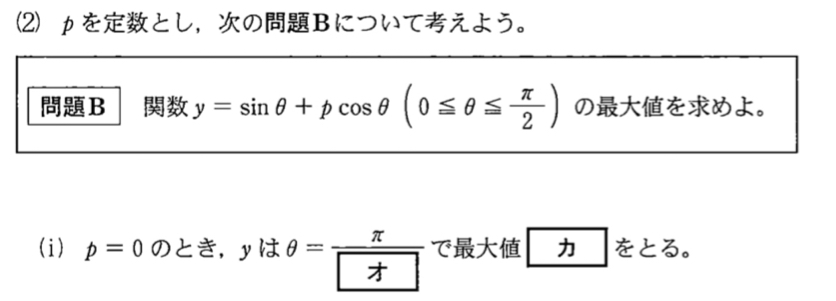
(２)( ⅰ )問題と解答・解説《オ〜カ》

解答・解説《オ〜カ》

$p=0$ のとき

$y=\sin \theta$ は $0≦\theta≦\displaystyle\frac{\pi}{2}$ において

$\theta=\displaystyle\frac{\pi}{2}$ で最大値： $1$ ・・・《オカ》

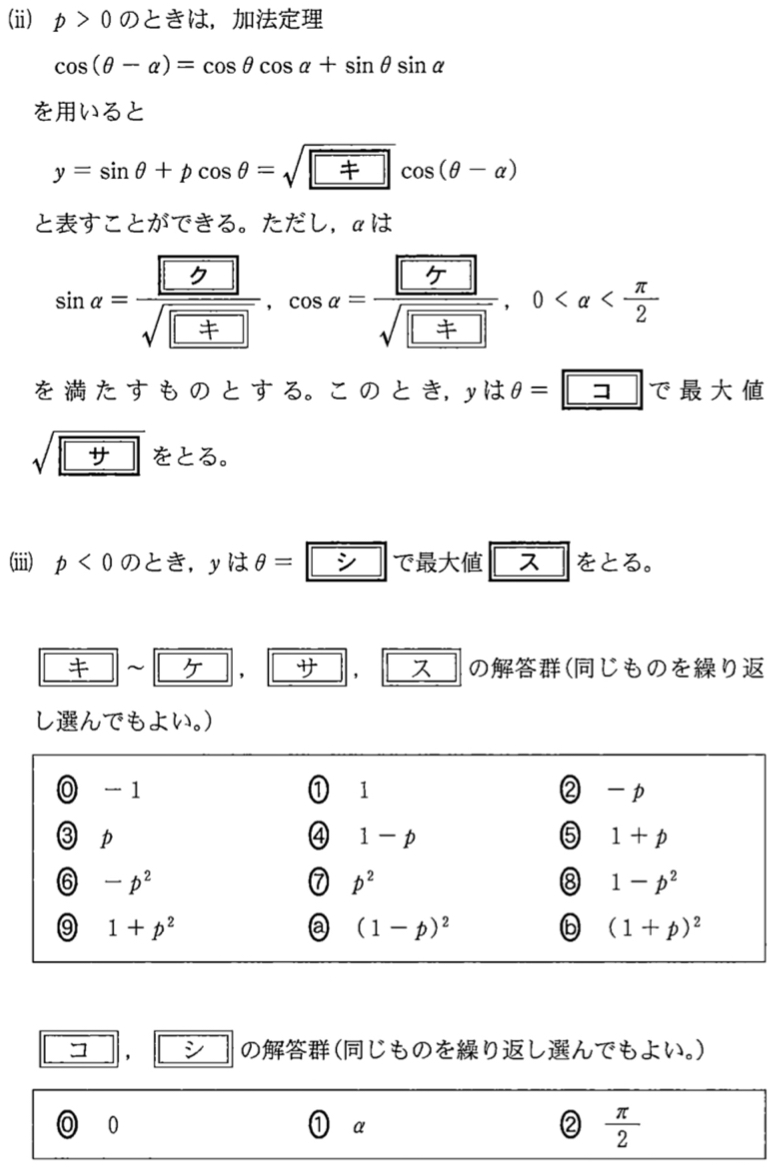
(２)( ⅱ ),( ⅲ )問題と解答・解説《キ〜ス》

解答・解説《キ〜ス》

( ⅱ )　$p>0$ のとき

$\sin\theta+p\cos\theta=\sqrt{1+p^2}\left(\cos\theta\cdot\displaystyle\frac{p}{\sqrt{1+p^2}}+\sin\theta\cdot\displaystyle\frac{1}{\sqrt{1+p^2}}\right)$

$\sin\alpha=\displaystyle\frac{1}{\sqrt{1+p^2}}$ , $\cos\alpha=\displaystyle\frac{p}{\sqrt{1+p^2}}$ ・・・《ク：①，ケ：③》

とすると与式は，

$y=\sqrt{1+p^2}\left(\cos\theta\cos\alpha+\sin\theta\sin\alpha\right)=\sqrt{1+p^2}\cos\left(\theta-\alpha\right)$ ・・・《キ：⑨》

と表すことができる．

よって，$0≦\theta≦\displaystyle\frac{\pi}{2}$ のとき

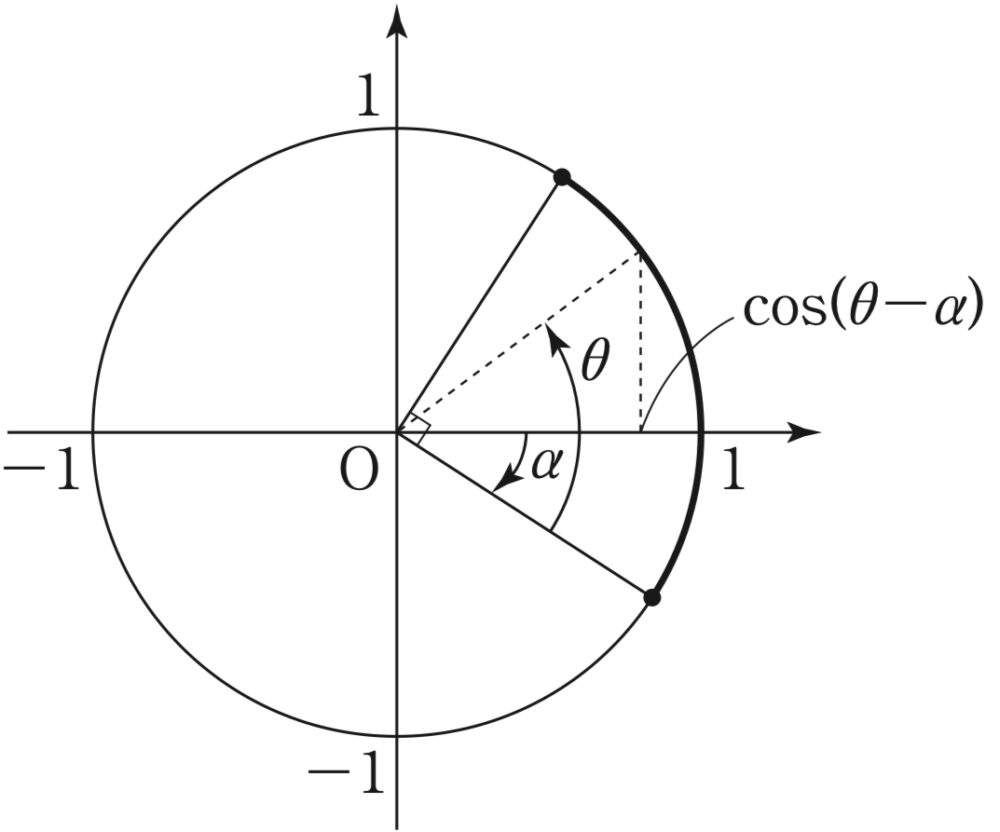$-\alpha≦\theta-\alpha≦\displaystyle\frac{\pi}{2}-\alpha$ なので

$y$ は $\theta-\alpha=0$

つまり，$\theta=\alpha$ で最大値： $\sqrt{1+p^2}$ ・・・《コ：①,サ：⑨》

( ⅲ )　$p<0$ のとき

$p=-q$ ( $q>0$ ) とおくと

$y=\sin \theta+p\cos \theta=\sin \theta-q\cos \theta$

$0≦\theta≦\displaystyle\frac{\pi}{2}$ のとき

$\sin \theta$ は増加，$\cos \theta$ は減少する．

$q>0$ より $y$ は増加する．

したがって，

$\theta=\displaystyle\frac{\pi}{2}$ のとき最大値：$1$ ・・・《シ：②,ス：①》

【2021共通テスト(第１日程)】数学ⅡB：第１問[２](指数・対数関数)｜会話形式から考察

太郎と花子の会話から、f(x)とg(x)の性質を考察する問題。相加平均・相乗平均の関係。大学共通テスト対策。センター試験過去問演習。数学ⅡB：指数・対数関数

mathmathmanabu.com

2022.09.16