【2023久留米大学・医学部】ランダムウォーク・推移グラフを利用した確率

考え方(ランダムウォーク・推移図の利用)

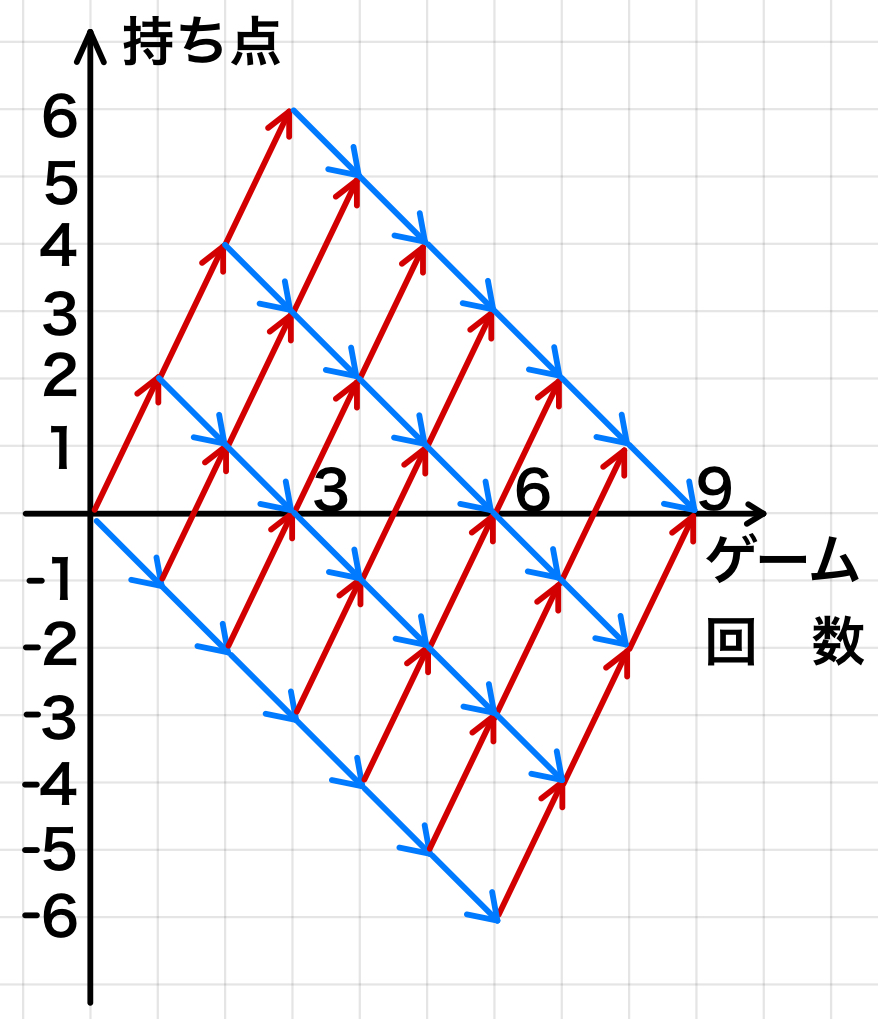
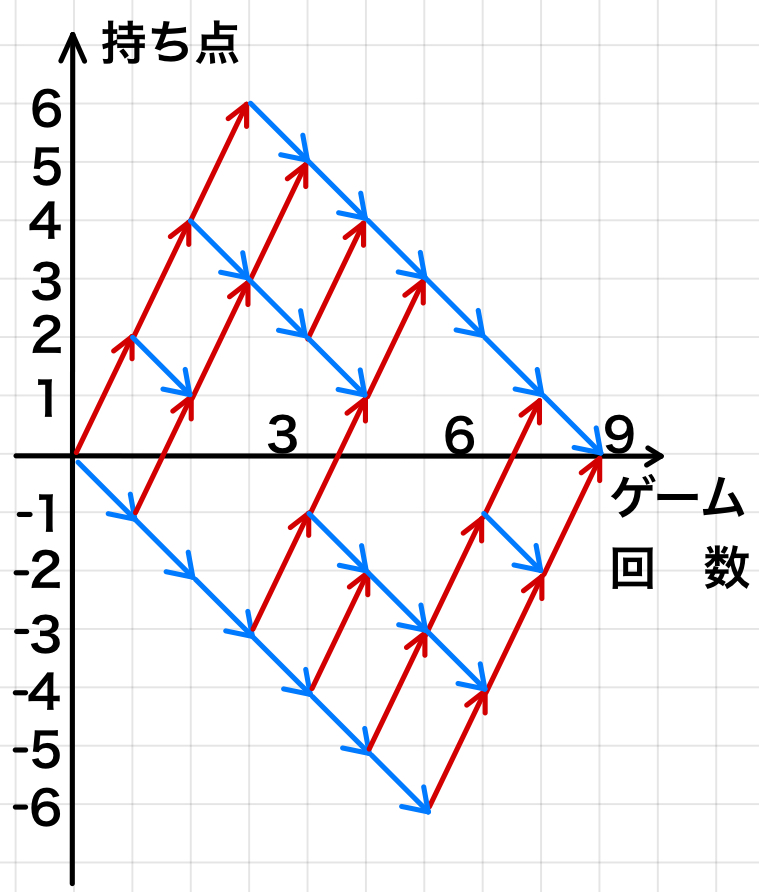
ゲームの回数と持ち点の変化は，下図のように表すことができます。

視覚的に捉えることで，数え間違い，漏れがなくなります！

※\(3\) の倍数の目が出た時は右上(赤矢印)，

\(3\) の倍数でなければ右下(青矢印) に動きます。

解答・解説

(１)　\(3\) 回目のゲーム終了時に \(0\) 点となる確率

\(1\) 個のサイコロを \(1\) 回投げ，出た目が \(3\) の倍数となる事象を \(A\)，\(3\) の倍数でない事象を \(B\) とする．

このとき，それぞれの確率 \(P(A)=\displaystyle\frac{1}{3}\) ，\(P(B)=\displaystyle\frac{2}{3}\) となる．

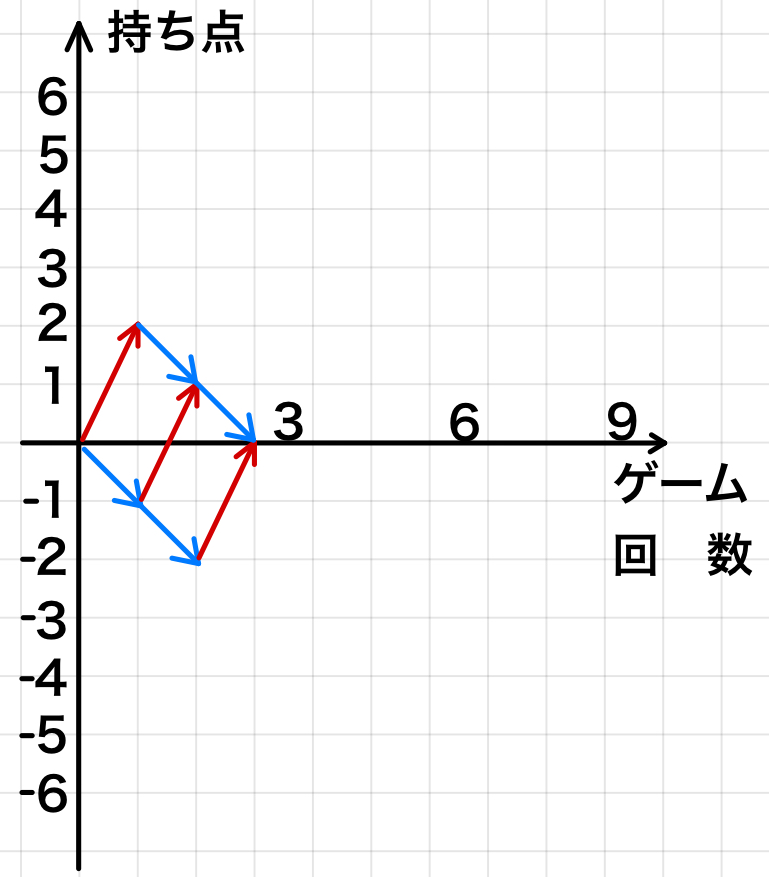右図のようにゲーム回数と持ち点を右図のように表すとき，

\((3,0)\) に到達するのは，\(3\) 回のうち事象 \(A\) が \(1\) 回，\(B\) が \(2\) 回起こればよいので，

\(_{3}C_{1}\left(\displaystyle\frac{1}{3}\right)\left(\displaystyle\frac{2}{3}\right)^2=\displaystyle\frac{4}{9}\)

(２)　\(6\) 回目のゲーム終了時にはじめて \(0\) 点となる確率

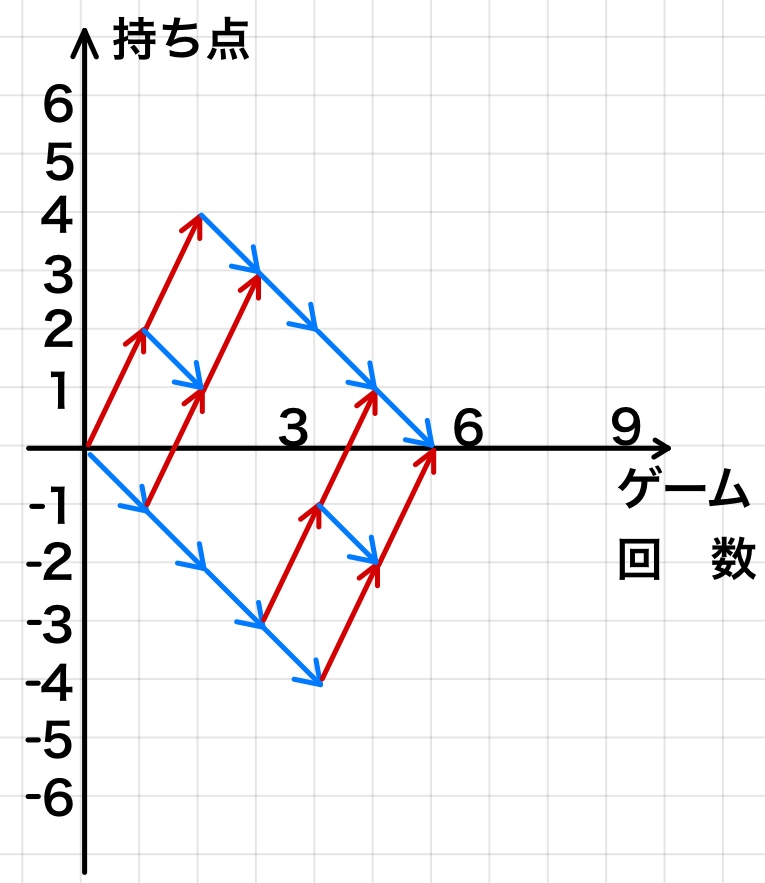\(6\) 回目のゲーム終了時にはじめて \(0\) 点となるのは，

\((6,0)\) に到達する全事象から，\((3,0)\) に到達したのちに \((6,0)\) に到達する場合を除けばよいので

\(_{6}C_{2}\left(\displaystyle\frac{1}{3}\right)^2\left(\displaystyle\frac{2}{3}\right)^4-\left(\displaystyle\frac{4}{9}\right)^2=\displaystyle\frac{80}{243}-\displaystyle\frac{16}{81}=\displaystyle\frac{32}{243}\)

(３)　\(3\) 回目のゲーム終了時に \(0\) 点になり，\(9\) 回目のゲーム終了時に \(2\) 回目の \(0\) 点となる確率

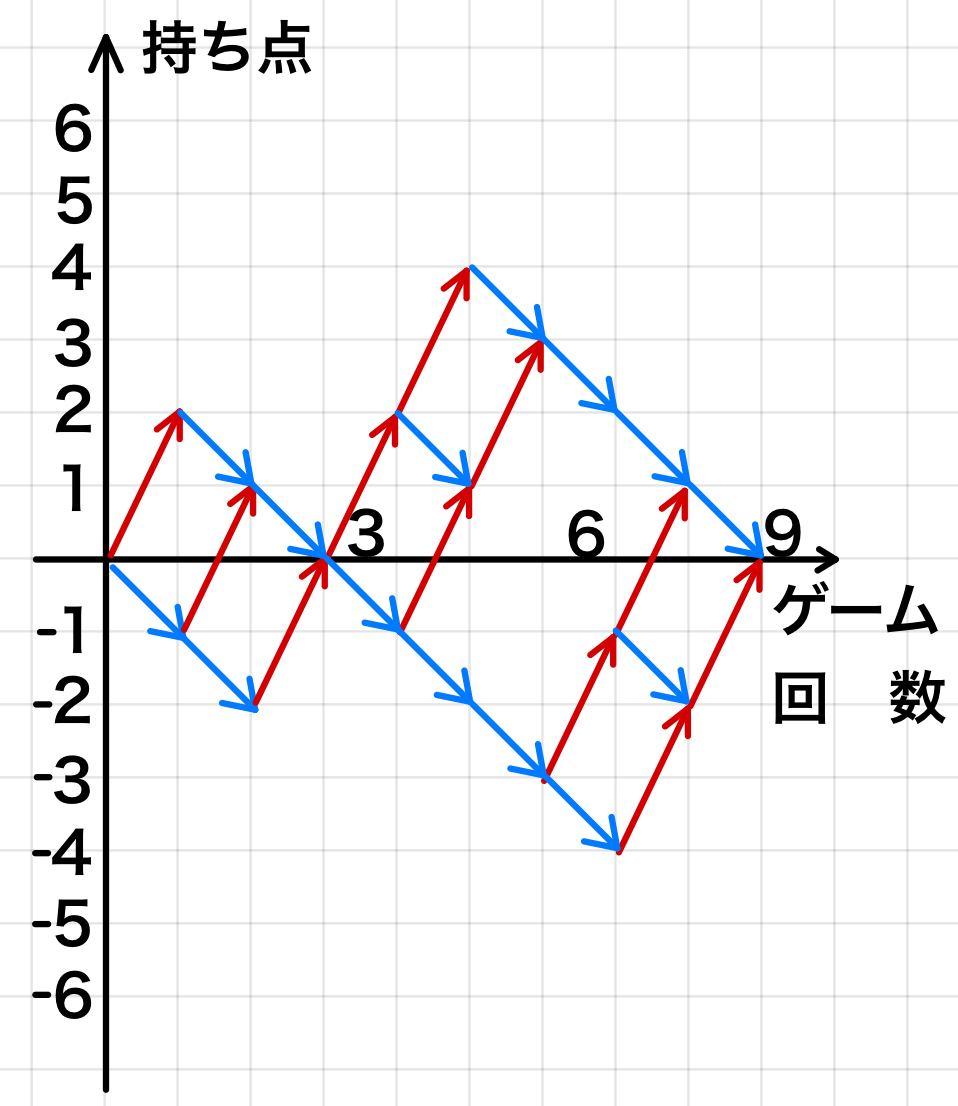
(１)，(２)の結果から

\(\displaystyle\frac{4}{9}\times \displaystyle\frac{32}{243}=\displaystyle\frac{128}{2187}\)

(４)　\(9\) 回目のゲーム終了時にはじめて \(0\) 点となる確率

まず \((9,0)\) に到達する確率は

\(_{9}C_{3}\left(\displaystyle\frac{1}{3}\right)^3\left(\displaystyle\frac{2}{3}\right)^6=\displaystyle\frac{1792}{6561}\)

この確率から，次の( ⅰ )( ⅱ )( ⅲ )を除けばよい．

( ⅰ ) \((3,0)\) と \((6,0)\) の両方を通る場合

( ⅱ ) \((3,0)\) のみを通る場合

( ⅲ ) \((6,0)\) のみを通る場合

( ⅰ )のとき

(１)の結果を利用すると

\(\left(\displaystyle\frac{4}{9}\right)^3=\displaystyle\frac{64}{729}\)

( ⅱ )，( ⅲ )のとき

いずれも(３)の結果に等しいので，\(\displaystyle\frac{128}{2187}\times 2\)

よって求める確率は，

\(\displaystyle\frac{1792}{6561}-\displaystyle\frac{64}{729}-\displaystyle\frac{128}{2187}\times 2=\displaystyle\frac{448}{6561}\)