【2021聖マリアンナ医科大学】
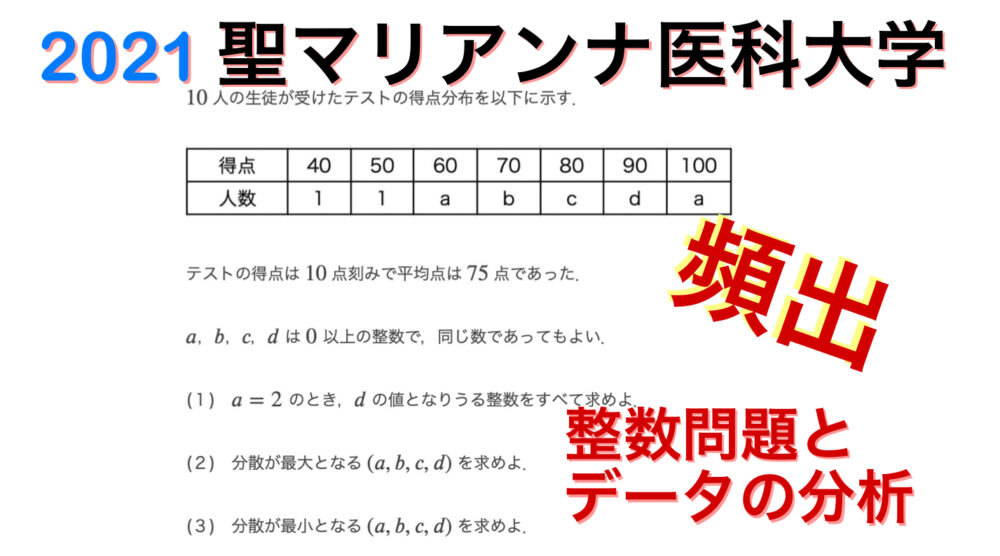
\(10\) 人の生徒が受けたテストの得点分布を以下に示す.

テストの得点は \(10\) 点刻みで平均点は \(75\) 点であった.
\(a\),\(b\),\(c\),\(d\) は \(0\) 以上の整数で,同じ数であってもよい.
(1) \(a=2\) のとき,\(d\) の値となりうる整数をすべて求めよ.
(2) 分散が最大となる \(( a , b , c , d )\) を求めよ.
(3) 分散が最小となる \(( a , b , c , d )\) を求めよ.
データの分析:基本公式の確認・まとめ
平均値
変量 \(x\) についてのデータが \(n\) 個の値 \(x_{1}\) , \(x_{2}\) , \(\cdots\) , \(x_{n}\) であるとき,それらの総和を \(n\) で割ったものを,データの 平均値 といい, \(\overline{x}\) で表す.
中央値,最頻値
データを値の大きさの順に並べたとき,中央の位置にくる値を,データの中央値(メジアン)という.
《例①》データが奇数個の場合
「データ:10 , 12 , 15 , 17 , 18 」の中央値は,「 15 」となる.
《例②》データが偶数個の場合
「データ:10 , 12 , 15 , 17 , 18 , 20 」の中央値は,15 と 17 の平均値をとった「 16 」となる.
データにおいて,最も個数の多い値を,そのデータの最頻値(モード)という.
分散と標準偏差
変量 \(x\) についてのデータが \(n\) 個の値 \(x_{1}\) , \(x_{2}\) , \(\cdots\) , \(x_{n}\) であるする.
また,\(n\) 個の値 \(x_{1}\) , \(x_{2}\) , \(\cdots\) , \(x_{n}\) の平均値を \(\overline{x}\) とするとき,
この値 \(s^2\) を分散という.また,\(\sqrt{s^2}\) を \(s\) で表し,標準偏差という.
と式変形することもできる.(証明は省略)

\(2\) 乗の平均,平均の \(2\) 乗から分散を求める公式は差がつきます!
演習問題として「【2021信州大学】相関係数の計算、分散=(2乗の平均)-(平均の2乗)の利用」をご参考に!
共分散と相関係数
\(2\) つの変量 \(x\) , \(y\) のデータが \(n\) 個の \(x\) , \(y\) の値の組として
\(( x_{1} , y_{1} )\) , \(( x_{2} , y_{2} )\) , \(\cdots\) , \(( x_{n} , y_{n} )\) のとき,
解説・解答
【2021聖マリアンナ医科大学】
\(10\) 人の生徒が受けたテストの得点分布を以下に示す.

テストの得点は \(10\) 点刻みで平均点は \(75\) 点であった.
\(a\),\(b\),\(c\),\(d\) は \(0\) 以上の整数で,同じ数であってもよい.
(1) \(a=2\) のとき,\(d\) の値となりうる整数をすべて求めよ.
(2) 分散が最大となる \(( a , b , c , d )\) を求めよ.
(3) 分散が最小となる \(( a , b , c , d )\) を求めよ.
テストを \(10\) 人の生徒が受けたので,
\(1+1+a+b+c+d+a=10\) \(\iff\) \(2a+b+c+d=8\)・・・①
また平均点は \(75\) 点であるから,
\(40+50+60a+70b+80c+90d+100a=75\times 10\)
\(\iff\) \(16a+7b+8c+9d=66\)・・・②
②ー①\(\times 7\) より
\(2a+c+2d=10\)・・・③
①ー③より
\(b-d=-2\) \(\iff\) \(b=d-2\)・・・④
\(b\) は \(0\) 以上の整数なので,④より \(d≧2\)・・・⑤
(1) \(a=2\) のとき
③より \(c+2d=6\) \(\iff\) \(c=2(3-d)\)

この式をただただ計算するのは大変!工夫をしましょう!
本問では,最大値・最小値となる \(( a , b , c , d )\) を求めることが目的ですから,不要な計算は省略していきましょう!
\(10s^2=(15^2+25^2)a+5^2b+5^2c+15^2d+\)(定数) と表せ,







コメント